
Welcome to Manifold plays chess, part 3.
This time, Manifold will play as white against Stockfish level 3 on lichess. Manifold lost both games so far, see https://manifold.markets/market/will-black-win-in-manifold-plays-ch and https://manifold.markets/citrinitas/will-white-win-in-alexliesmans-mani for these games.
This market resolves YES if white wins.
This market resolves NO if black wins.
This market resolves to 50% if there is a draw.
The game will unfold here: https://lichess.org/GF9YULQP
The game so far: 1. e4 e5 2. Bc4 Nf6 3. Nc3 Nc6 4. Nf3 Nxe4 5. Nxe4 d5 6. Bd3 dxe4 7. Rg1 Bf5 8. Bb5 exf3 9. Bxc6+ bxc6 10. Qxf3 Qd7 11. Qc3 f6 12. g4 Bxg4 13. Rxg4 h5 14. Re4 Qd5 15. Qf3 Rd8 16. d3 a6 17. b3 Qc5 18. Kd1 a5 19. Bb2 g6 20. Qxf6 Kd7 21. Rxe5 Qd6 22. Qxh8 Be7 23. Qg7 Rf8 24. Rxe7+ Qxe7 25. Qxe7+ Kxe7 26. Ba3+ Kf7 27. Bxf8 Kxf8 28. Kd2 Kf7 29. Re1 Kg7 30. Re7+ Kf6 31. Rxc7 h4 32. a4 g5 33. b4 Ke6 34. axb5 Kd6 35. Rb7 Ke6 36. a6 Kd5 37. h3 Kc5
Market for current move:
Market structure:
Per move, there will be a free response market, followed by conditional markets for 2 or 3 moves. The free response market will resolve to the move that manifold will play. For each response, the average probability in the last four hours before close is measured. With 75% probability, two moves will be randomly drawn, with weight proportional to those market probabilities. With 25% probabilities, three moves will be randomly drawn in the same way. Then for each of the two or three candidate moves, a conditional market is created.
If there are 3 or less legal moves, no free response market will be created, and we directly move to the conditional markets.
The markets for the candidate moves are of the form "What will the score be one move later if we play X?". We measure the average probability in the last four hours of the market. The move with higher probability wins and gets chosen. The conditional market that does not get chosen gets resolved N/A. The conditional market for the move that gets chosen resolves to the score one move later.
The score is the average probability in the last four hours of trading in the conditional market for the winning move. If there is no later move, the score for this purpose is 1.0 - #moves x 0.0004 if white win, 0.5 - #moves x 0.0002 if its a draw, or 0.0 if we lose (this is to encourage a shorter game).
In the first 6 moves, the moves "Resign1", "Resign2", "Resign3" will be legal moves (and white loses immediately if it plays one of those moves). After that, any resign move will not be legal.
Possible rule changes during the game:
If the probabilities for the conditional moves stagnate, I plan to introduce some kind of leverage, so that predictors can predict in a wider range. An example for what I mean by leverage: if the score stagnates around 0.65, we could map 0.6 to 20%, and 0.7 to 80%, and interpolate for the rest. These changes will be announced at least 2 moves in advance.
Other than that, I reserve the right to change some of the rules during the game, if the game becomes very boring or if I am concerned that funding the remainder of the game will become too expensive. In that case, I do not attempt to change the outcome of the game. For example, if the score is below 0.01 over many moves, I might add a mechanism that allows us to resign.
I will wait for 1-2 days before starting the game, during which the rules might be changed.
Edit (2023-03-05): changed description to clarify rules slightly, no changes were made to the rules.
Edit (2023-03-05): Accidentally deleted the paragraph about Resign moves in the previous edit. Added again.
Edit (2023-03-06): Changed "This market resolves NO if white wins." to "This market resolves NO if black wins."
🏅 Top traders
| # | Trader | Total profit |
|---|---|---|
| 1 | Ṁ891 | |
| 2 | Ṁ781 | |
| 3 | Ṁ462 | |
| 4 | Ṁ133 | |
| 5 | Ṁ78 |
We did it! For the first time, Manifold won a game of Manifold plays chess. Thank you for participating!
Things that I might do different for next time:
- resolve conditional markets to main market (average over some pre-determined times)
- probably don't do the move penalty for score
- only create 2 conditional markets each move - not clear that 3 markets were better
- do the average over the last hour instead of last 4 hours
- use some mechanism that the worse conditional market has a chance to resolve. like 1% or 2% probability the losing move gets chosen. But bigger chance if the conditional market outcomes are very close to each other.
However, I will not run Manifold plays Chess 4 anytime soon (and I decided on that before I lost all my mana if you ask). If others want to run that, or run another game, now might be a good time. Maybe I can even help you in some way.
@harfe Thanks for running the game! I had fun seeing how the game and the market mechanism played out and manipulating them for some profit. :)
https://manifold.markets/harfe/manifold-plays-chess-3-if-we-play-4-b9b5d11507a2
potentially last market
https://manifold.markets/harfe/manifold-plays-chess-3-move-41-what-c06064831380 we could win very soon
Wow this market is optimistic! Please predict here:
https://manifold.markets/harfe/manifold-plays-chess-3-move-30-what
https://manifold.markets/harfe/manifold-plays-chess-3-move-29-what pls predict and/or choose moves
https://manifold.markets/harfe/manifold-plays-chess-3-move-28-what Our opponent has only 5 pawns and a king left. How should we continue?
I am considering testing "leveraging", as mentioned in the "possible rule change during the game". Originally the idea is due to @citrinitas (I forgot where). See also some discussion here.
Why? The score of the conditional markets are stagnating, and profits are low. The game looks to be relatively calm. Also I would see this as an experiment, rather than a thing that improves accuracy.
Downsides: This would mean additional complexity and would make it more complicated to understand for participants how the mechanism works in detail.
@harfe as for the concrete transformation formula, I am not sure. One considerations is to have a market value of 0.1 correspond to a score of 0.7, and linearly interpolate for the rest (with a market value of 0.0 corresponding to a score of 0.0 and 1.0 corresponding to 1.0). With the additional rule that we drop back to un-leveraged markets once the score goes below 0.7 (upon resolution).
@harfe I think the most manipulation-resistant resting point for the leverage is at 0.5 -- at either end, it becomes proportionally cheaper for an attacker to shift the market towards 50%. I'm not super confident about that, though.
Most things I've said about manifold chess are collected at https://manifold.markets/post/manifold-plays-chess-2-retrospectiv
@citrinitas interesting argument. That was also an alternative I considered in the discussions with Daniel: choose the transformation so that the previous score corresponds to a probability of 50%. Downside is that the formula changes every move, which might make things even more complicated.
>market value of 0.1 correspond to a score of 0.7
In this model a neutral 50% market value would correspond to a score of 0.8333 which I think is too high for a neutral market in the current game position (there’s still many ways to blunder white’s advantage as shown by one of the current move candidates). Making the neutral 50% correspond to a score of 0.7 would be more sensible, imo.
>the most manipulation-resistant resting point for the leverage is at 0.5
Can you unpack this a bit for me? What is resting point, is it related to the recent score of 0.7-0.75? And are you saying that should correspond to a 0.5 (50%) market, similar to what I suggest above?
>Downside is that the formula changes every move
In our discussion you proposed having the same formula and I liked the simplicity, except we’d revert back if the score tanked, like you suggested here. And it can be piecewise linear (though I like me a smooth curve, which btw I think I fixed the error I had made with that first suggestion). You had mentioned something like (0.1,0.9) mkt prob <-> (0.65,0.85) score, and interpolate the rest. What’s the downside of this for all moves (as long as score>.65)?
@deagol Resting point is what I'm calling the value that the conditional markets should resolve to, if there is no change in the evaluation market.
I think the most "mathematically pure" way to work this would be with a log-odds transformation. For example:
import math
Logit = float
Prob = float
def log_odds(p: Prob) -> Logit:
return math.log(p / (1-p), 2)
def inv_log_odds(l: Logit) -> Prob:
return 2**l / (1 + 2**l)
def score_market_resolution(eval_prior: Prob, eval_posterior: Prob) -> Prob:
scale_factor = 1.0
return inv_log_odds(scale_factor * (log_odds(eval_posterior) - log_odds(eval_prior)))
for prior, posterior in [(0.7, 0.8), (0.7, 0.7), (0.7, 0.4), (0.4, 0.7)]:
score = score_market_resolution(prior, posterior)
print(f'{prior} -> {posterior} == score {score}') results in
0.7 -> 0.8 == score 0.6315789473684211
0.7 -> 0.7 == score 0.5
0.7 -> 0.4 == score 0.2222222222222223
0.4 -> 0.7 == score 0.7777777777777777Here raising the 'scale_factor' makes the leverage stronger without disrupting the smoothness of the curve.
This feels like the kind of thing where some Robin-Hanson-esque grad student proves it's optimal for some condition under certain constraints, and then it turns out you violate those constraints in the real world but it performs pretty well anyway.
But I haven't done any of that analysis and I'm just going on vibes, so take this with a grain of salt.
@harfe I think the result is getting close to ordained now, so might as well experiment away!
@citrinitas yeah, it’s pretty much what I was trying to get to here (stumbled by trying to use a generalized logistic which broke the 50% symmetries) but as I mentioned above I think I got it right now. The only difference is I think you swap the concept we’ve been using as ‘score’ with the conditional resolution value. This is what I got for the smooth score as a function of its winning conditional’s last 4 hours average probability p, the previous move score s, and a leverage factor L:
score(p) = 1 / ( 1/odds(s)/odds(p)^(1/L) + 1 )
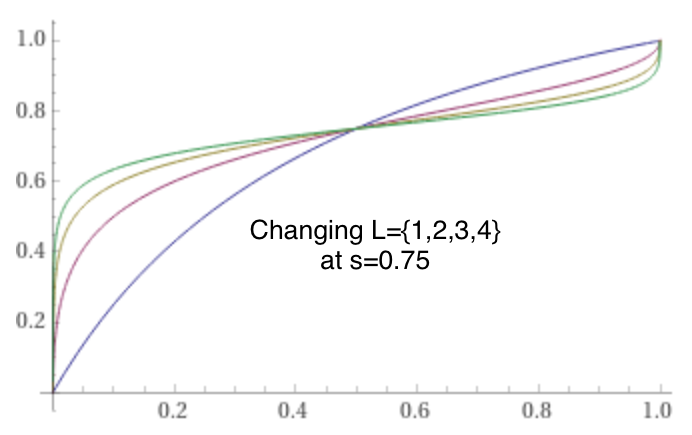
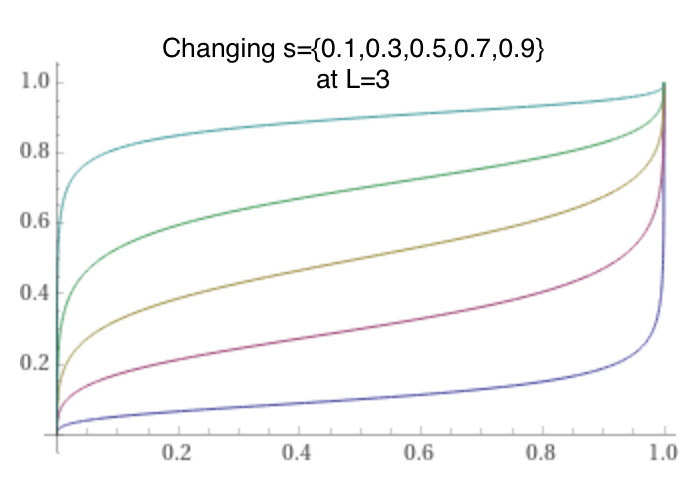
I can’t prove that’s mathematically pure or optimal, just, same as you it seemed sensible to multiply the odds of the conditional (scaled) by the odds of the previous score, then invert the logit. But then @harfe prefers the piecewise linear, which I don’t mind.
One reason why I like piecewise linear: linearity is nice because it plays well together with expected value. piecewise linear also does break linearity, but at least it is locally preserved.
Another argument against leveraging that just came to mind: if the market values are more extreme at close, it means a higher portion of the subsidy gets in the pocket of traders. And currently at near 80% it is more extreme than it might be with leveraging. But its a cost I can live with.
Ok preliminary decision now:
Starting move 31 I will introduce a piecewise linear transformation function to convert market values into scores (I called this leveraging originally. Not sure if this is a good name actually).
The market will be centered around 50%, that is if z is the (possibly rounded) score of the previous move, z will correspond to a market value of 0.5.
Other score-market interpolation points are (z - 0.08, 0.1) and (z+0.08, 0.9). If z>0.9, then we use transformation as if z=0.9 (similar rule if z<0.1). We will automatically return back to normal when the difference between consecutive scores is greater than 0.08 twice in a row. I reserve the right to switch to a different formula or to the normal way but will announce this 1-2 moves in advance.
@harfe “We will automatically return back to normal when the difference between consecutive scores is greater than 0.08 twice in a row.”
I’m not following this bit, can you explain?