Self-embed so you can see the histories of probabilities: [TODO]
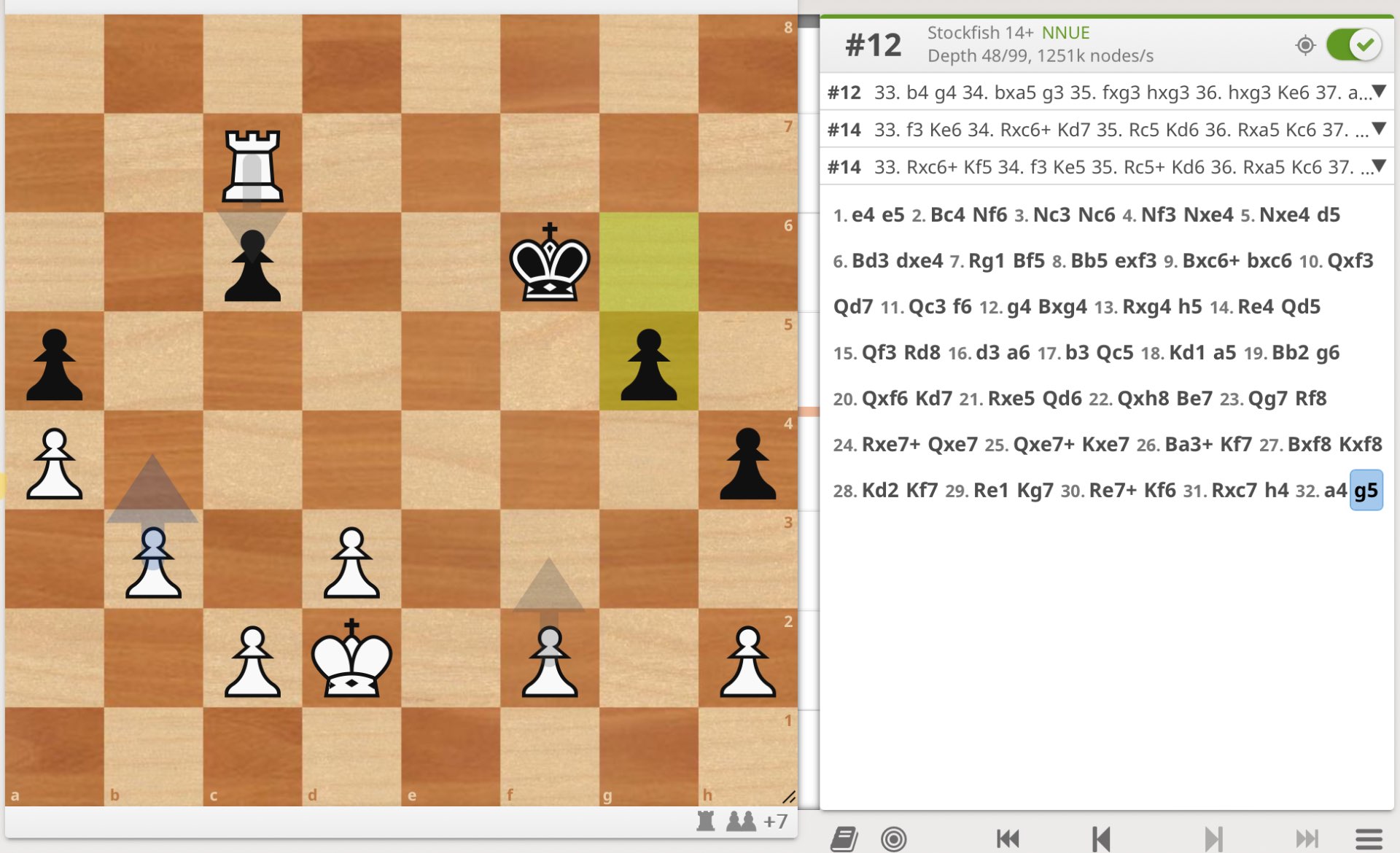
What will white (Manifold) play in move 33?
Check the game here: https://lichess.org/GF9YULQP
The game so far: 1. e4 e5 2. Bc4 Nf6 3. Nc3 Nc6 4. Nf3 Nxe4 5. Nxe4 d5 6. Bd3 dxe4 7. Rg1 Bf5 8. Bb5 exf3 9. Bxc6+ bxc6 10. Qxf3 Qd7 11. Qc3 f6 12. g4 Bxg4 13. Rxg4 h5 14. Re4 Qd5 15. Qf3 Rd8 16. d3 a6 17. b3 Qc5 18. Kd1 a5 19. Bb2 g6 20. Qxf6 Kd7 21. Rxe5 Qd6 22. Qxh8 Be7 23. Qg7 Rf8 24. Rxe7+ Qxe7 25. Qxe7+ Kxe7 26. Ba3+ Kf7 27. Bxf8 Kxf828. Kd2 Kf7 29. Re1 Kg7 30. Re7+ Kf6 31. Rxc7 h4 32. a4 g5
market for previous move:
For each response, the average probability in the last four hours before close is measured. With 75% probability, two moves will be randomly drawn, with weight proportional to those market probabilities. With 25% probabilities, three moves will be randomly drawn in the same way. Then for each of the two or three candidate moves, a conditional market is created. The average probability in the last 4 hour of the conditional markets will be measured. The move with higher average probability will be chosen.
More details here:
https://manifold.markets/harfe/will-white-win-in-manifold-plays-ch
Any resign moves or draw offeers are not allowed in this move!
Invalid moves or duplicate moves will be removed from consideration.
🏅 Top traders
| # | Trader | Total profit |
|---|---|---|
| 1 | Ṁ145 | |
| 2 | Ṁ31 | |
| 3 | Ṁ6 | |
| 4 | Ṁ4 | |
| 5 | Ṁ2 |
Moves by average probability:
0.622116 b4
0.176240 Rxc6+
0.061370 Ke3
0.000000 h3 (removed)
--------------------
pick a number between 1 and 999999998 (inclusive)
Outcomes by integer range:
[ 1-542485330] b4, Rxc6+
[542485331-792485330] b4, Rxc6+, Ke3
[792485331-974376523] b4, Ke3
[974376524-999999998] Rxc6+, Ke3
Hash of the complete table:
d3fe440f28d7ac5e117fec1c7f422e9957a346ff1e66efbab023278542d1d41e
@jack just let it think deeper or play a couple of moves, eventually it sees it. I get #12 with a4, #14 with the others.
It’s baffling to me that such a simple pawn gambit, which pays off within a dozen moves, should require this ridiculous depth for the engine to even consider it.