
Check the game here: https://lichess.org/GF9YULQP.
The game so far: 1. e4 e5 2. Bc4 Nf6 3. Nc3 Nc6 4. Nf3 Nxe4 5. Nxe4 d5 6. Bd3 dxe4 7. Rg1 Bf5 8. Bb5 exf3 9. Bxc6+ bxc6 10. Qxf3 Qd7 11. Qc3 f6 12. g4 Bxg4 13. Rxg4 h5 14. Re4 Qd5 15. Qf3 Rd8 16. d3 a6 17. b3 Qc5 18. Kd1 a5 19. Bb2 g6 20. Qxf6 Kd7 21. Rxe5 Qd6 22. Qxh8 Be7 23. Qg7 Rf8 24. Rxe7+ Qxe7 25. Qxe7+ Kxe7
The other candidate move is 26. Ke2
The conditional market for the other move is here:
If the value (averaged over the last 4 hours before close) of this market is higher than in the other market, then this market resolves PROB to the score after move 27. Otherwise, it resolves N/A. The score after move 27 is the value (averaged over the last 4 hours) of the conditional market of the winning move in move 27.
Note that when the game ends, the score will be 1.0 - #moves x 0.0004 if white wins, 0.5 - #moves x 0.0002 if its a draw, or 0.0 if we lose.
More details for the overall game here:
https://manifold.markets/harfe/will-white-win-in-manifold-plays-ch
🏅 Top traders
| # | Trader | Total profit |
|---|---|---|
| 1 | Ṁ6 | |
| 2 | Ṁ0 |
@deagol Still unsure. Current candidate:
market value 0.15 <-> score 0.65
market value 0.85 <-> score 0.85
And the rest linearly interpolated.
Another option would be something more adaptive, where the score of the previous move corresponds to a market value of 0.5.
@harfe In the more adaptive option, if the target central score (from the previous move or avg last two or whatever, call it T) corresponds with the market at 50%, to what score do other market values correspond to? I mean, something like score(mkt) such that score(.5)=T. And then later on seems we’ll need the inverse of this function in order to resolve the leveraged markets? Or am I misunderstanding how this all works? Perhaps you have a simple linear interpolation function in mind but it isn’t obvious to me.
I did some algebra using a logit transform with quite hairy but interesting results, consider this:
score = ( odds^(-1/L) + 1 )^( ln(T)/ln(2) ) where,
odds=mkt/(1-mkt)
L>0 a leverage shape parameter
0<T<1 the target central score such that score(mkt=.5) = T
I graphed it with a few values for L (2 to 5) and T (.1 to .9) and it seems right. But I suspect the intuition of the market probability driving the score, which in turn drives the game result prediction will get lost with this much complication, and no one will be eager to play with this monster?
@deagol so this function won’t work, I must have messed up my assumptions, a bad substitution, or fudged the parameters somewhere. The mkt vs 1-mkt market symmetry is not being preserved for extreme T, the correct functions should be the same but rotated 180 degrees when changing T with 1-T but they instead appear flipped, though seems leverage helps make them more similar.
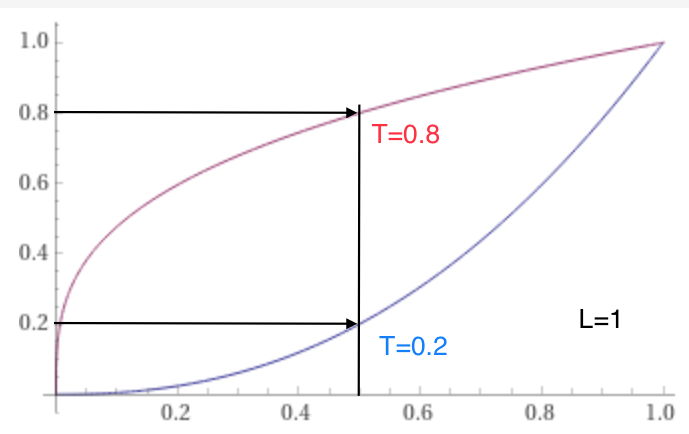
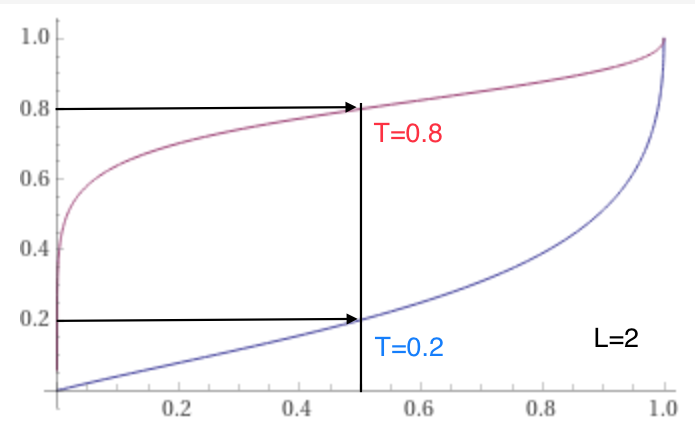

@deagol I think piecewise linear is better than a smooth curve. I was thinking like score(0.5)=T, score(0.9)=T+0.1, score(0..1)=T-0.1, with exception when T is <0.13 or >0.87.
@harfe ok got it, thanks, and I guess obviously score(0)=0 and score(1)=1. But why the exception at .13/.87? I’m thinking the more rule exceptions, the less intuitive it gets.
@harfe to clarify exactly how this would work around move 29:
The winning market for move 38 (call it m28) resolves as usual, to the score after m29, so betting on m28 centers around T=score_m28=avgProb4h_m28.
However the score after m29 isn’t the usual “last 4h avg probability of the winning m29,” (avgProb4h_m29) but rather the leverage-transformed version of that average around 50% mapped around T: score_m29=T+(avgProb4h_m29-0.5)/4 | 0.1<p<0.9, so betting on m29 centers around 50%. And now we set this score as the new T=score_m29 (call it T29).
But that means the resolution of m29 can’t be to “the score after m30,” but rather back to a de-levered version of score_m30 (to realign the predictions that were centered around 50%). What exactly is this transform? Is it just the avgProb4h_m30?
We again would have: score_m30=T29+(avgProb4h_m30-0.5)/4 and if m29 simply resolves to that raw avgProb4h_m30 winning average, it seems to me the back-propagation of the predictions gets weakened, since that m30 average is intended as a judgement on the current move’s (m30) relative improvement, not the previous move (m29), yet it’s delta from 50% would be used to pay off the previous move’s (m29) bets. I’d instead propose m29 should resolve (call it R29) to the de-levered version of this score_m30 but using the previous move’s central parameter T28 instead (indeed score_m28), since that was the presumed “central aim” of predictions made in m29, in a way, “how far should the score move away from T28:” R29=0.5+4*(score_m30-T28).
Note this isn’t the same as the winning average avgProb4h_m30, but something a bit more involved. Not sure if I’m clearly explaining the potential disconnect in the back-propagation that I’m trying to avoid with this tweak. I quickly get lost and muddied with the game theory equilibrium logic, and I’m being far from rigorous here.
Similarly, betting on m30 and beyond would happen at around 50%, and resolve to a de-levered version of the score after the next move, but using the previous move’s central parameter (which is same as the score after the previous move).
Sorry for the length, but I think we need to get the exact computations right so that informed predictions can be truly predictive and not just whimsical guessing. How all this gets communicated in the conditionals or the game’s main market, is a whole other story.
@deagol You convinced me to delay this for at least one move (because I would need to write some code).
(Answer for 3.: The transform is the inverse function of the original transformation function).
I think you mostly have it right, but let me try a framing that makes it more clear, hopefully:
Every market has a market value (mkt) and a corresponding score. One can calculate score from mkt with a function f: score = f(mkt). There is also an inverse function g, which allows us to calculate mkt from score: mkt = g(score). The functions f, g can be different for each market.
When a market closes, I will calculate mkt as the average over the last 4 hours, and then calculate and announce score for this market.
When a market resolves, I take the score of the winning market of the next move. Then calculate mkt from that score. Then resolve it to that.
As for communication, I plan to publish a table of (mkt, score) values for each market.
@harfe Yes that makes it way more clear, thanks. So the question I was trying to express is on the resolution of any market,
>take the score of the winning market of the next move.
>Then calculate mkt from that score.
>Then resolve it to that.
In the second step mkt=g(score), it’s not clear which g to apply (note that “functions f, g can be different for each market“). Is it the one from the next winning move market or from the market being resolved? If it’s from the next winning move market, by definition of inverse function you get back mkt=g(score)=g(f(mkt))=mkt (the 4h avg prob so resolution is same as usual), and I suspect it becomes more like a self-resolving market. But what I’m suggesting is to use the prior move’s g (the one being resolved) applied on the next winning move score, since I suspect the “50% center” shifting at each move may break the predictive connection between moves, and I think this lag reintroduces that predictive chain. But I’m not 100% sure of this, maybe I’m wrong and the raw mkt avg probability already incorporates the past moves predictive power.
@deagol Yes, good point, I did not clarify that.
The function g gets taken from the market that is being resolved. If f_29, g_29 are the functions that belong to market of move 29, then to resolve market 29, we calculate the score after move 30 using f_30(mkt_30), and then resolve market 29 to the corresponding PROB calculated by g_29(f_30(mkt_30)). This can be different from mkt_30 if the markets use different functions.
@deagol Maybe it might be better to use the same function for all markets, for example centered around 75%.
@harfe I do prefer the simplicity, and I assume if bettors pick a blunder and the score tanks, the function would change again?
@harfe I’d also like to read what others think of these changes, how they feel about the current problem of stagnating scores making it hard to profit on such small changes, and whether the proposed solution is worth making the structure even more complicated
@harfe here’s yet another idea: word the conditional questions in terms of changes to the score
“If we play <move>, how much will the score change from the current <score>%? (delta from 50%)”