TLDR: how likely is it that on the eve of the election, Manifold Politics will assign probability X% of a Republican (obviously Trump in almost all scenarios) winning the Presidency? How much uncertainty do you have? Reshape the distribution to match!
Details:
OK, this is a relatively nerdy market.
I'm curious about how confident Manifold is in its estimates of the presidential race. (For example, users who expect important news cycles ahead should have a flatter probability distribution, predicting that the race has a good chance of moving in either direction rather than staying still.)
There are some markets like this already (see the earliest comment), but I think Manifold's numeric question type makes for better incentives and more granular results!
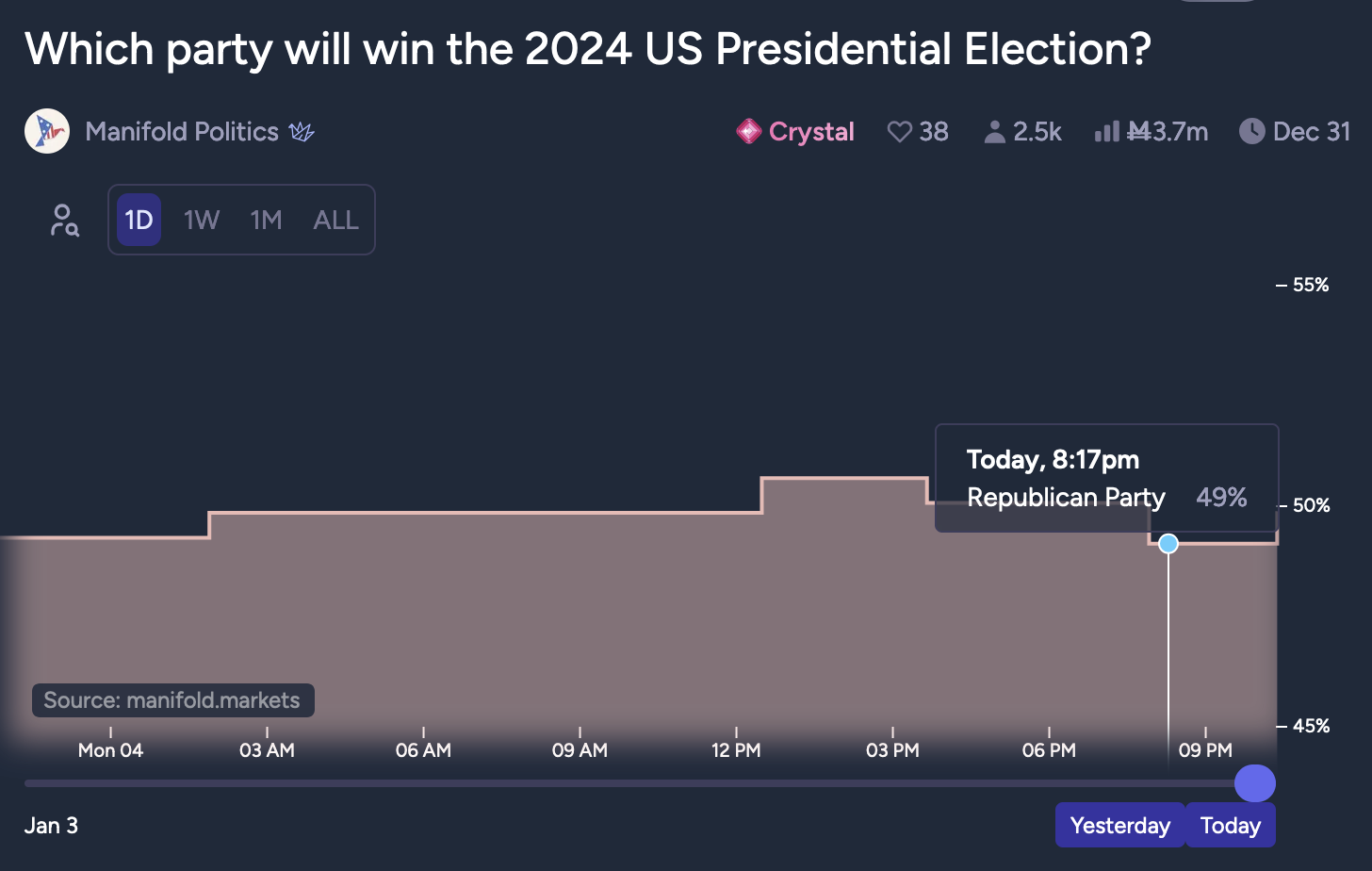
This market will resolve to the median of the minute-by-minute values for the Republican Party in the Manifold Politics presidential market between 23:00 and 23:59, Eastern time, on November 4th. (That should be fairly resistant to wild swings.)
If Manifold crashes during that time, I will instead use the values from the last hour preceding the crash.
This market will close at noon on November 4th, to prevent it from becoming too much of a game of reflexes in the final hours.
🏅 Top traders
| # | Name | Total profit |
|---|---|---|
| 1 | Ṁ2,875 | |
| 2 | Ṁ1,589 | |
| 3 | Ṁ1,136 | |
| 4 | Ṁ676 | |
| 5 | Ṁ576 |
People are also trading
I am having trouble resolving this market, and would like help ASAP!
The transaction log for the market appears to be broken: it ends several minutes before the hour that I'd like to analyze.
If anyone finds a way in the next few hours to extract useful numbers such that I can take a median and possibly get a number, I will use that to resolve this market.
Otherwise I will use the hourly-granularity value of 50, and deem both [47.5, 50] and [50,52.5] to be correct.
Nice, I didn't even know this market format existed
I did a similar market for the night after the election and one for when the market reaches a confident decision
https://manifold.markets/MichaelBlume/when-will-manifold-decide-the-elect
https://manifold.markets/MichaelBlume/what-will-be-the-probability-on-wil
I think if this were a 10-bucket add-to-1 market for n ≤ val < n+10, with the probability assigned to [90,100] being just 2.9%, you'd similarly be unable to profit by buying YES individually on each bucket besides that one. But that market would give you the option to bet NO on that one bucket, and unfortunately that's what seems to be missing here. I hope they add that feature to markets like this one.