I don't know of any source that specifically claims their AI has received at least bronze but not gold on the IMO, and has given enough information that at least establish that they solved it within the time limit.

I think the "bronze medal grade" on the Gemini Model Card is not enough information. If that would be enough, then the headline of the 2024 AlphaProof announcement ("AI achieves silver-medal standard") should also be enough information to resolve this YES. When more details were provided, it was decided that AlphaProof 2024 didn't qualify.

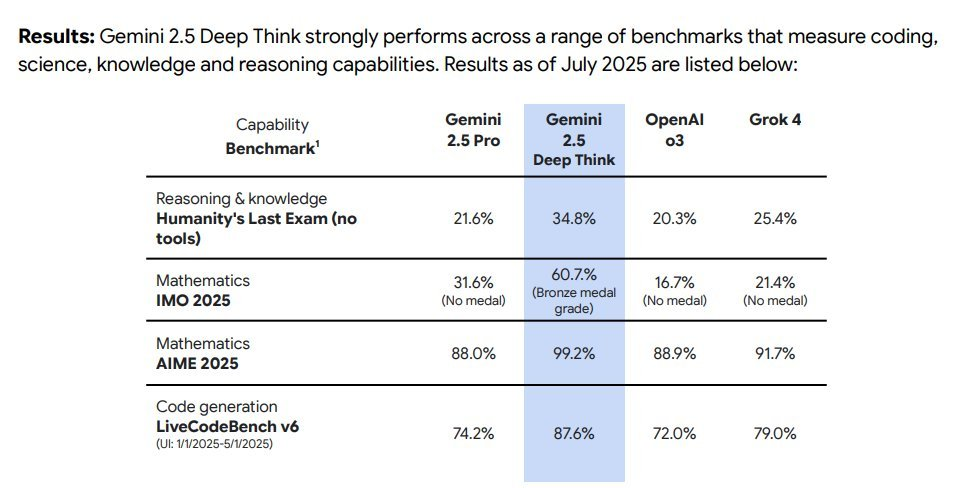
Google's DeepThink was frequently said to be Bronze level iirc?

I can't quite find it confirmed on twitter but eg reddit says this and i remember reading this from goog ppl

https://www.reddit.com/r/Bard/comments/1mi3pz2/comment/n70xsjj/?utm_source=share&utm_medium=web3x&utm_name=web3xcss&utm_term=1&utm_content=share_button

from the Gemini 2.5 Deep Think Model Card

@Bayesian This is compelling, but I am confused that 60.7% is not actually a natural multiple of 1/42

Edit: Perhaps this line from immediately above explains it: "To reduce variance, we average over multiple trials for smaller benchmarks."

@Forrest do you agree with this meeting the criterion for positive resolution?

I have a pretty substantial stake in this market, and it seems like it's going to come down to a moderator's judgement, so I am hesitant to make more trades or express opinions too strongly, feel free to consider this post talking my book.

That said, I think these are the best arguments against the Deepthink model card counting:

• Clearly the IMO was evaluated multiple times and the results were averaged. If we count a bronze/silver performance on this average for the purposes of this market, it seems like it could bias towards a YES resolution relative to just basing it off of a single evaluation: if the model would sometimes get gold and sometimes not medal, these could average out to a bronze score. If we knew exactly what happened on the first pass of evaluation, we would have something more in line with the idea of a single evaluation of a model, but it seems that that information isn't available in the model card.

• In Paul Christiano's pinned comment on the linked market, most of the criteria mentioned would seem to be met by this, except for maybe a couple:

  • Christiano says that there's no partial credit for answers - I don't see any mention that the model card graders applied this standard, and I don't see a big reason to think they would (other than if they maybe knew about the bet and were trying to copy the criteria). Christiano said he expected to trust the conclusions of the lab graders, but it seems to me that this was in the context of expecting one big attempt for gold where it would be possible to see individual question grades later and determine if they were doing things this way.

  • Christiano says he would give a team the benefit of the doubt for not adjusting their system if the attempt occurred within a week of the IMO. IMO ended July 20 and the model card was published August 1, so it's hard to say for sure if when the attempt happened, it was within a week, or whether that would be important. Given that Deepthink was accessed through "the Gemini App", it's not clear to me that bias in the form of small adjustments to high-level human-decided parameters was something that Google as an entity was trying to avoid - perhaps regular adjustments were being made by one team based on usage data while another team was doing the evaluations.

.

bytedance seed is also a silver no?

@typeofemale Do you have a good reason to think that they completed in the time limit, rather than after three days as I argued below?

@BoltonBailey I think there is a lot of baseless speculation on this subject

@BoltonBailey I guess I should also say, I saw this comment where the authors were directly asked about the time limit, and one says that within the time limit "many useful lemmas have been proved", which seems to somewhat confirm to me that they are not saying that the entire problems were proved in this time frame.

The "(but not gold)" in the title was added afterwards? Can I get a refund for this?

Also how does it resolves now? If an AI get gold and another get bronze or silver and not gold, it should resolve YES right?

@BAUEREsaie The creator left a comment a few years ago saying that if one AI got gold then this would only resolve YES if another AI got silver or bronze (I guess it's not ideal that this wasn't in the title or criteria until recently, but I also think that these rules are a reasonable interpretation of the original title).

@BoltonBailey Okay this answer my last two questions.
I'm still confused about the change in the title, it feels that before the edit the question would resolve YES if an AI wins silver AND gold, and now that it would resolve NO.

Here's my assessment of where things stand:

• OpenAI got gold, and so by the creator's comment below, it doesn't count for this market.

• Google Deepmind also got gold.

• Harmonic claimed gold in their announcement, and also they technically said they took more than 4.5 hours on some problems, so I think their attempt wouldn't count by the standards of Austin's market anyway.

• Numina did not solve any problems, per this tweet

• Bytedance seed prover claims silver, but seems to indicate by their announcement (translation) that they spent 3 days on the problems, which would be over the time limit.

The only thing is that Thomas Zhu made a comment in the Bytedance announcement thread on the lean zulip that Huawei had "claimed 34/42 (backed by a quote from IMO)" but "could only find relevant news in Chinese". I can't find any reference to this myself, seems weird that it would be so low-profile that it doesn't exist in english-language media.

@BoltonBailey I found a source on Chinese media claiming so, https://news.yesky.com/hotnews/12/305512.shtml is one

Just search up something like "华为IMO银奖" on Baidu to find more ads that just talk about that.

They posted their solutions on Github https://github.com/huawei-xiaoyi/IMO2025-solutions

I saw this line in a bunch of news articles:

IMO主席Gregor Dolinar教授对华为AI的表现给予了高度评价:“华为AI提交的答卷获得了34分(满分42分),这是一个了不起的成就。(The Huawei AI scripts received a grade of 34 out of 42, which is a remarkable result.)”

Roughly translated as:

Professor Gregor Dolinar, President of the International Mathematics Organisation (IMO), spoke highly of Huawei AI's performance: "The Huawei AI scripts received a grade of 34 out of 42, which is a remarkable result."

@bohaska Thanks for finding this! I note that (my Google translation of) the article says:

After three days of intense competition, Xiaoyi successfully solved five of the six difficult problems

Which makes me think, similar to seed prover, that this is technically not in the 4.5 hour competition time frame. But I guess we might need the market creator to weigh in.

Oh no this won’t happen idk what past me was thinking

(to clarify: they'll get gold, and nobody will report the shame of only getting silver)

@Bayesian I mean, DeepMind already reported having their AI win silver, with only 1-2 points behind gold. Are you saying no one will do it again?

https://deepmind.google/discover/blog/ai-solves-imo-problems-at-silver-medal-level/

(The reason it didn't count was because their AI used too much time compared to the actual length of an IMO.)

@Bayesian Oh, clever. I do think there will be reasoning models which do get bronze or silver, even if they aren't reported on. Like people will just run o3 on the problems and report how it does; those might be sufficient to resolve.

@AdamK Plausible yeah.

@Forrest Did an AI get bronze or silver on any International Math Olympiad by end of 2025?

This is based on another market, which is based on a bet between Christiano and Yudkowsky, so if either of them mention an opinion on what should count, I'll probably defer to it.

As far as I'm aware, there are two issues which might be considered to disqualify the recent attempt: the use of manual translations to Lean, and the fact that it exceeded the time limit by roughly a factor of 15.

It is my current opinion that the 'translations' issue does not disqualify the attempt for the purposes of this market, but that the 'time limit' issue does, and thus that the criteria for YES have not yet been met.

However, I have not looked into the topic in depth yet, and cannot promise that I won't change my mind as a result of more research (nor will I promise to do said research in a timely manner - sorry)

Would be a good idea to have all of that in the description, seeing as this question as of today resolves YES. Thank you.

If there's been news today specifically, what I said above may be out of date.

I feel that having this in the comments is probably good enough, but will admit that if I were a better market creator I'd've given an opinion sooner.

there's not been news today, the official is just doing word gymnastics