🏅 Top traders

📢POLL RESULTS
77.8% Multi Binary

11.1% Leagues

11.1% Newsfeed

📢I have given a poll to manifold staff. Should know in 24 hours to resolve this.

Is there a plan for how to resolve these "most impactful feature" markets ?

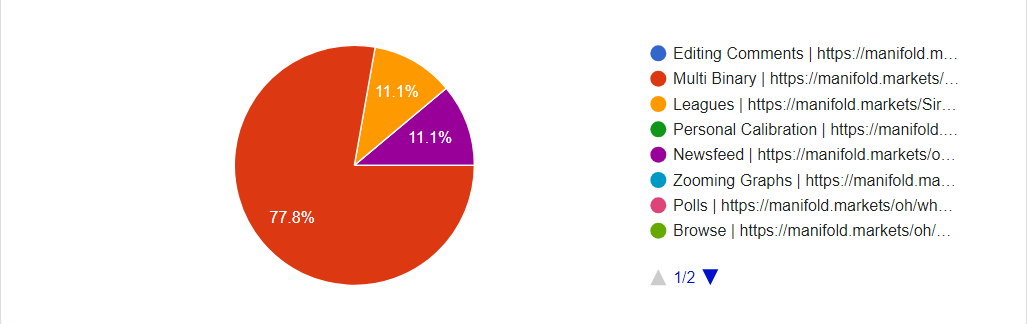
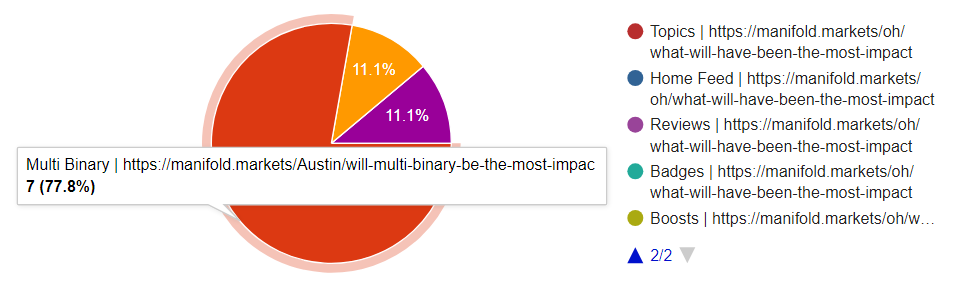
Of the 40 biggest markets on the site by total traders, 9 were created after this market was posted. Of those 9, four (almost half) were multi-binary.

Of the 400 biggest markets on the site by total traders, 111 were created after it, and 26/111 are multi binary.

Of the 4000 biggest markets, 1469 were created after it, and 194 of them were multi binary.

It seems like, even though multi-binary isn't used as much for generic markets (13%), it has an outsized impact on top markets (23% for top 100, 44% for top 10).

And this specifically means that, of the markets that get attention on sites outside manifold, multibinary has had a massive impact. There are two markets that I remember as big events manifold recently - the speaker market, and the sam altman firing market. Both are multi-binary. The altman market is one of the few markets I've comes across on social media entirely divorced from manifold. The latter corresponds to a visible spike on the unsmoothed daily active users graph - from 1.6k to 2.7k users - a 60% jump, enabled by one feature! What other feature did that?

Can anyone name a new feature this year that's even of comparable impact

@jacksonpolack I agree. I find myself porting existing markets to the multi binary format. This is the best feature I've seen added to the site despite the initial buggy start. Great job, absolutely love it.

People who are not on manifold don't care about leagues, and new users are not enthusiastic about leagues from the get go. But multi-binary? A random twitter user is capable of understanding them and being excited about it. Easy to use. Still has flaws but imo the best feature this year.

@firstuserhere Multi binary has so much potential. We don't yet have the ability to do an early resolve NO of linked markets. We don't have support for "at least one" or "at most one" or "exactly four". We can't split or combine answers. I think it will end up being the 2023 feature that has by far the largest 2024 impact.

It's 'most impactful', not 'very impactful'. I agree it's had less impact than one would've hoped, but I can't think of another feature that's had a similar level of impact

Leagues is fun, but realistically it's mostly helped retain the top traders somewhat more than otherwise.

@jacksonpolack I largely agree, I'm only betting down to 69%. There's also the indirect impact by helping enable Manifold Love.

@jacksonpolack eh I disagree. I like multi binaries, but they've got a ton of small problems that make them less valuable to traders (and it shows): unlinked ones have terrible liquidity distributions, linked ones have terrible ratio and display distribution at any significant scale, there's no ability to switch on or off submissions, shortform display in search and portfolios is meaningless and incomprehensible, and traversing limit orders is a nightmare.

why do those matter? because no matter how much we like these types of markets, they're not popular with traders. Binary markets are significantly more popular, even where they're less efficient. Look at those numbers about super popular MBs: the reality is that multi binaries get an order of magnitude more house liquidity injection per trader but it doesn't improve the liquidity experience enough to compete with binaries. if they rimpact full, more impactful, we wouldn't see them making a dent at the top of the curve, we'd see them taking over at the base.

@Mira Big fan of the news dashboard?

Will this market be N/A'ed if multi binary doesn't come out this year?

@xyz I guess that's moot

Since this is essentially grouping multiple binary markets, will this support partial resolution? That is, resolving one of the binary markets but not others.

Suppose I'm running a contest and anyone can submit an entry. Right now, I wait until the end of the month to judge them, because if it's rejected people would sell their answers if I did it while the market was open. Instead with this it seems like I could add a binary market to the group, and resolve it NO leaving the others intact?

Another one might be "When will X event occur?" where you want to keep resolving monthly markets NO as time passes(maybe closing them in advance so people don't just sell out) until the event occurs and you get a YES.

Another reason is just keeping the list organized, so people know an option isn't possible.

I predict everyone would want to trade these as much as possible if they could get rolling payouts.

Now offering a bounty of 10k mana if you can find this closed form solution for our constant product market maker:
https://manifoldmarkets.notion.site/Bounty-for-CPMM-closed-form-for-buy-amount-given-shares-936e629e676d4590a853d65f03d20786

With this closed-form equation, we can remove the last binary search within the inner loop of our multiple choice arbitrage code. Right now, it takes 42 ms on my macbook to arbitrage between 3 answers. With this solution it should take ~1ms, which should allow us to run it even on the client.

@JamesGrugett Spent an hour on this so far, it's a much harder problem than it looks at first glance...

@MayMeta yeah, the fact that p is not fixed really makes this more complicated than it might have needed to be. There are other accounting identities they could use which would allow p to remain unchained during liquidity provisioning. I am not certain why or if Manifold must use such a novel market mechanism in their cpmm.

Even for specific p I'm suspecting we won't improve on binary search here. For example, if p=1% then the solution involves the root of a 100th-degree polynomial!

@dreev Wow, thanks guys for trying!!

For the new multiple choice, we are planning to fix p=0.5, so I will award the 10k mana just for that solution!

@JamesGrugett Oh, that one's easy! 1/2*(s-y-n+Sqrt[4*k^2 + (n-y+s)^2])

PS: Or rewriting that without k and with the YES vs NO cases separately:

1/2*(s-y-n+Sqrt[4*n*s + (y+n-s)^2])

1/2*(s-y-n+Sqrt[4*y*s + (y+n-s)^2])

@dreev Wow! Thanks a ton. I will confirm it today and then send you a manalink!

@JamesGrugett We can still offer another 10k mana for the full solution of a general p, though I'm not sure whether we need it.

I see @dreev has made a market on whether it'll be solved!

I don't think it makes sense to award the bounty for the p=1/2 case because just pasting into WolframAlpha gives you that one!

@dreev I agree, I assumed the general solution is needed, when I was trying to solve it. The 0.5 case is trivial.

@dreev @MayMeta Ok, thanks for weighing in! I guess I won't award the M10k for just the p=0.5 case since that's a little unfair to anyone who didn't see my message immediately.

Separately, I have tested @dreev's solution and it works! Thanks for your help!
You all have my gratitude at least.

@JamesGrugett interesting. Fixing p=0.5 initializes each of the n markets at 50% each so you will total n/2. However if you are fixing p then I think you will be rebuilding the liquidity provisioning mechanics in which case I very much favor the multiasset cpmm

@ShitakiIntaki We can actually start each sub-market off with 1/n probability by changing up the yes and no shares initially in the pool. There's a way to maximize use of the initial liquidity because we know that only one answer will resolve YES — which means we can distribute more YES shares than we could otherwise between all the answers.

BTW, I've reduced the arbitrage calculation to one overall binary search that is taking just 3 milliseconds (for an admittedly simple case)!! Those closed form solutions are doing magic.
I've so far only implemented the case for buying YES in an answer, but it includes limit orders.

@JamesGrugett I seem to proved that a general closed form is impossible. Details coming later after I double checked.

@giojoai I think that deserves the prize.

@giojoai Details have been posted to the Discord server.