Resolution:
I will split markets into creators bet / creators didn't bet.
From there I will split markets into buckets (2.5% confidence, 10% confidence, ..., 90%, 97.5%).
Within each bucket, I will calculate the beta distribution posterior for each bucket, using Beta(0.5, 0.5) as the prior (because it's the Jeffreys prior).
I will calculate (analytically if it's not too much trouble, numerically if it is) the KL divergence between the actual posterior and the best possible posterior for the number of markets in the bucket.
Finally I will take the average of all the KL divergences, weighted by the number of markets (so if there are no markets in a particular bucket, we ignore the fact that the KL divergence will be zero)
The "better calibrated" predictor will be the one with the lowest average KL divergence.
For the first 24 hours of this market, these resolution criteria are subject to change if anyone makes a convincing argument that I should modify this procedure in some way. (e.g. use something other than KL divergence (I don't see why, "bits of information to move to perfect calibration" seems like a good measurement), or "you need to normalize in some other way to avoid biasing the measurement").
(What I would like to do is model each group as a Beta process and then measure the average KL divergence between the processes and a hypothetical perfectly calibrated predictor, but quite frankly that is too much work)
If for some reason the calculation is not feasible, or I realize while doing it that I've messed up and it's not a valid comparison, market will resolve N/A.
🏅 Top traders
| # | Name | Total profit |
|---|---|---|
| 1 | Ṁ117 | |
| 2 | Ṁ16 | |
| 3 | Ṁ6 | |
| 4 | Ṁ4 |
People are also trading
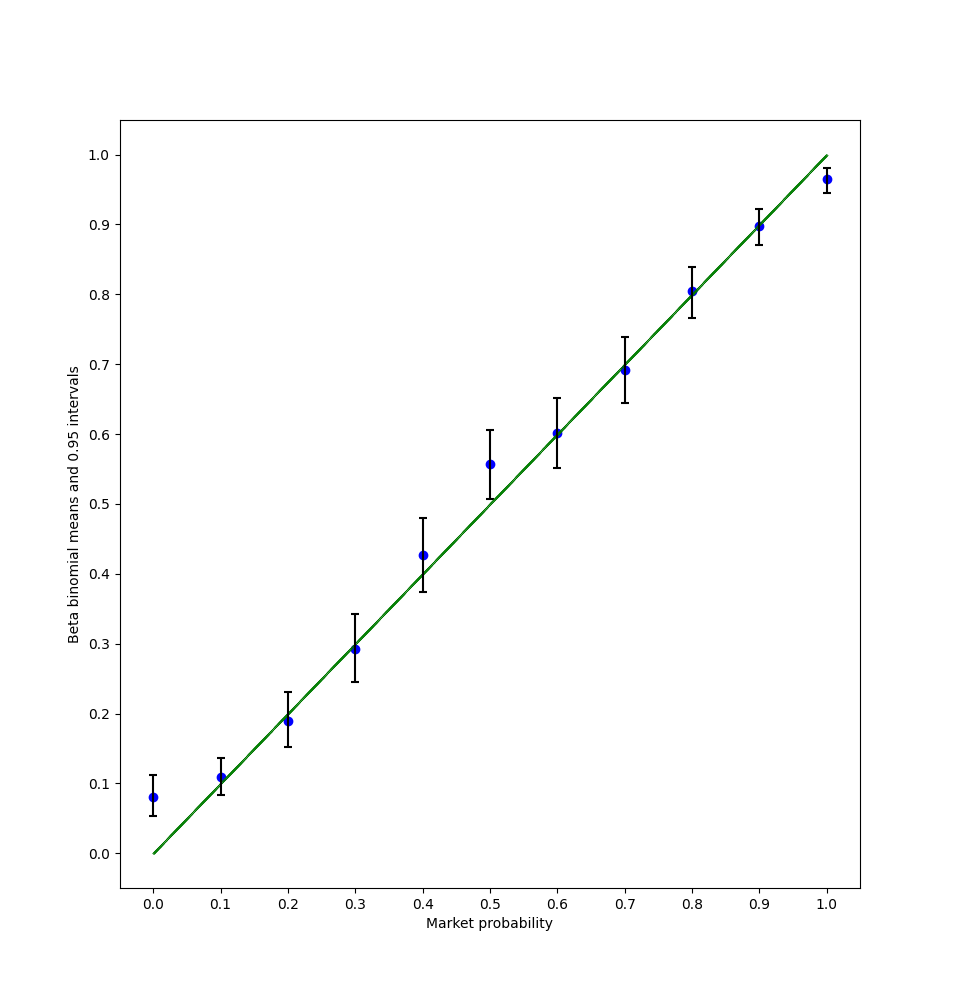
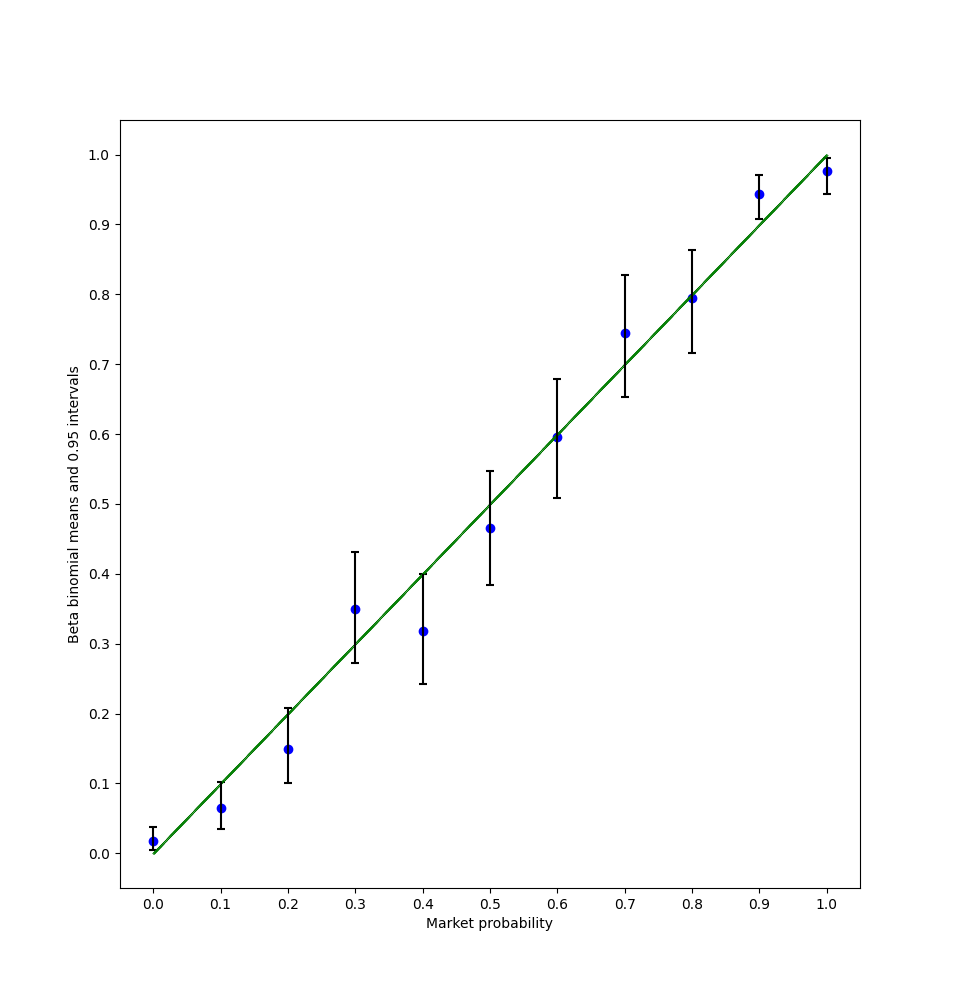
KL divergence with creator bets: 1.29
KL divergence without: 0.91
Note that I filtered out markets with fewer than 5 trades: these were very obviously skewed in the no creator bets group (specifically the 50% and 90% buckets were fucked).
I decided not to take a weighted average, because the lower number of markets actually does represent real uncertainty and that should be taken into account.
@egroj Ah, sorry, soon - I have been busy and have not had time to write the analysis. I'll do it this week once I'm at a computer again.
@TheSkeward Ah, sorry. This will be for every binary and free response market that resolved to a single answer (not N/A or prob). These are the markets where I've written the tools to calculate a well-defined market probability.