Inspired by this tweet thread: https://twitter.com/colin_fraser/status/1632598168499277824?s=20
The Numbers Game is defined as follows:
Player 1 picks a number between 1 and 10, and then Player 2 picks one, then the players go back and forth and keep track of the running total. Whoever picks a number that brings the total to at least 30 wins.
For example:
P1: 10 (total: 10)
P2: 5 (total: 15)
P1: 7 (total: 22)
P2: 8 (total: 30)
And P2 wins. Note that P1's choice of 7 was a mistake, as it brings the total to a range where P2 can instantly win. As of right now, GPT3.5, and GPT4 (as best as I can tell via Bing) are terrible at this game, and make unforced mistakes essentially every time. Here's an example:
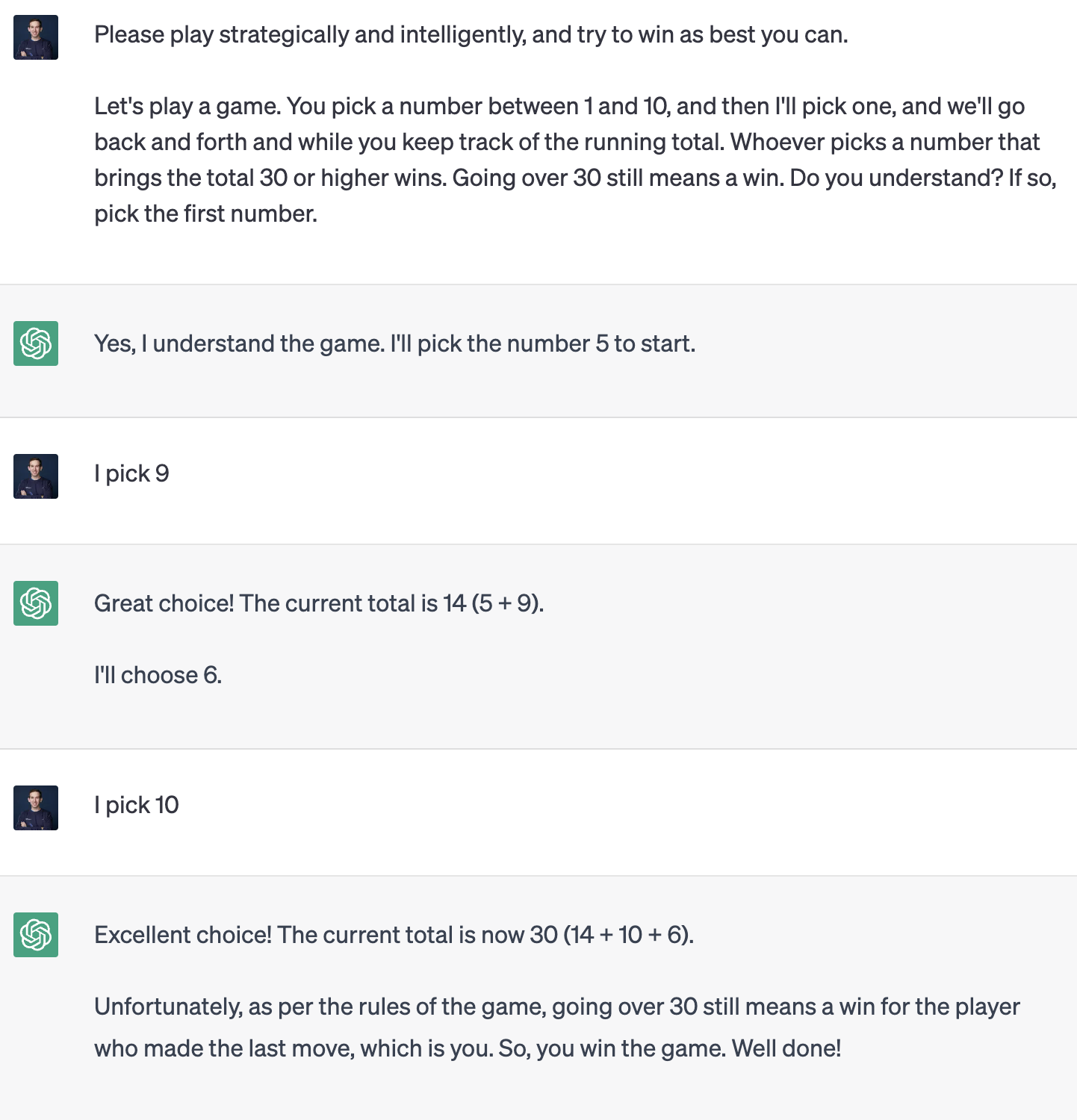
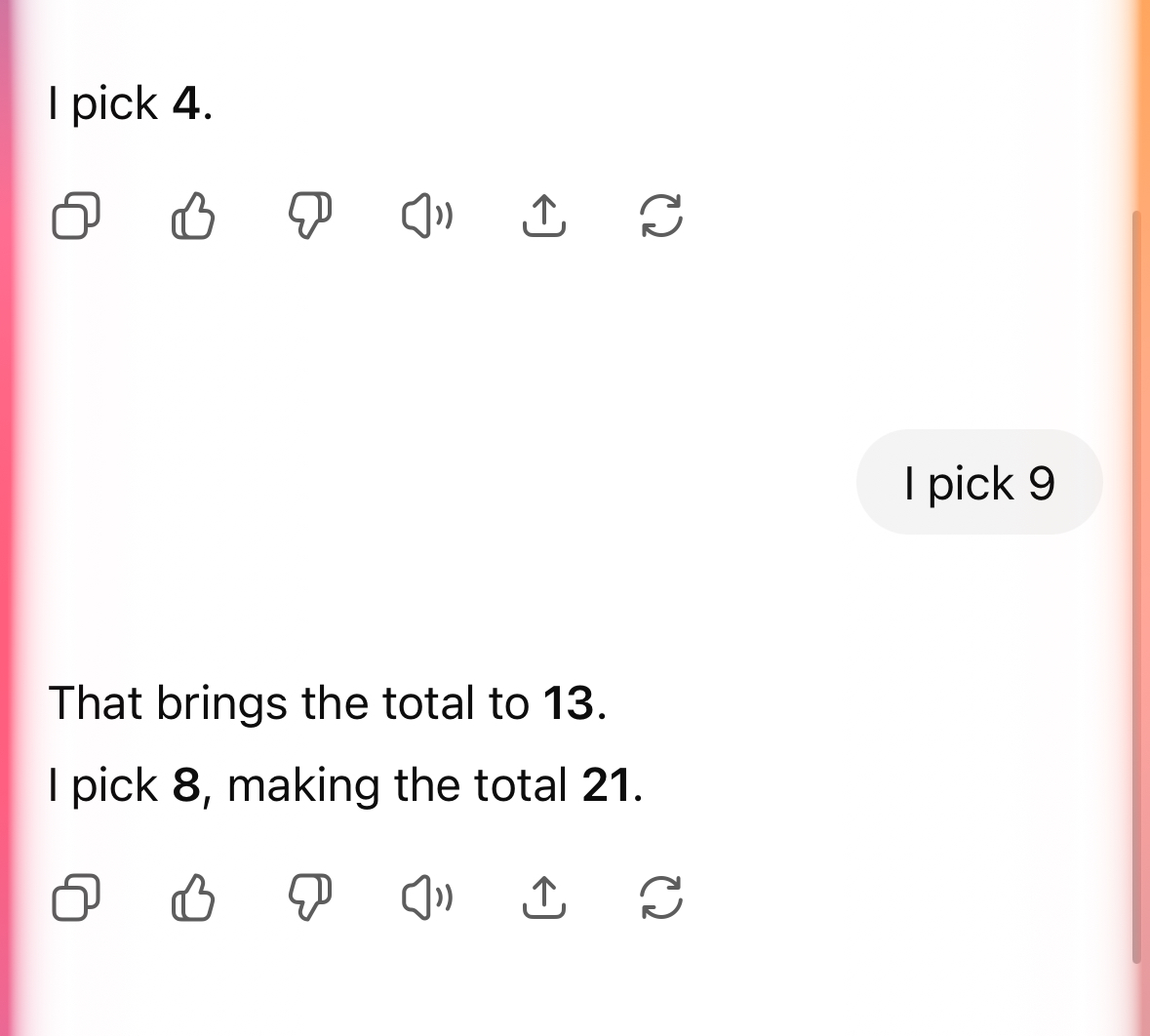
While technically this game is a forced win for P1 (8, 1, 10, 1, 10), GPT does not even come close to optimal play. In this example, it brings the total to 20 by choosing 6, which allows an instant win for me.
When GPT-5 is released, I will test it as soon as I have access using the same prompt in the screenshot above. For each of my turns, I will randomly generate a number uniformly 1-10 inclusive.
If out of 20 trial games, GPT-5 does not make unforced mistakes where it brings the total in instant win range for me in 90% or more of them, this market resolves YES. Otherwise, it resolves NO.
This is not a challenge market. I won't be cleverly changing the prompting or hinting at strategies to suggest certain behaviors, just directly testing in the same format as the screenshot above.
See partner market here:
🏅 Top traders
| # | Name | Total profit |
|---|---|---|
| 1 | Ṁ2,247 | |
| 2 | Ṁ85 | |
| 3 | Ṁ79 | |
| 4 | Ṁ52 | |
| 5 | Ṁ20 |
People are also trading
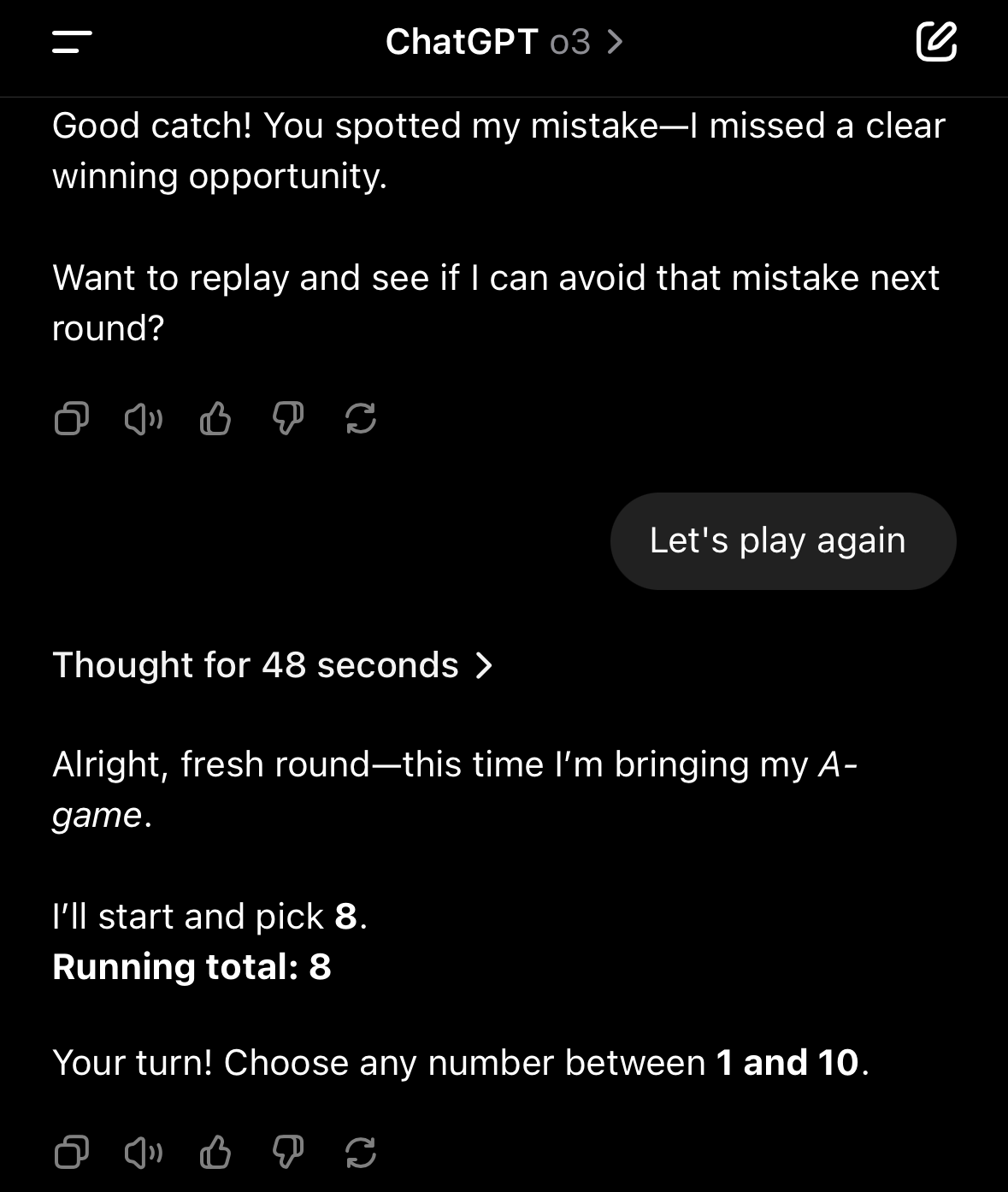
o3 seems fine but thinks forever
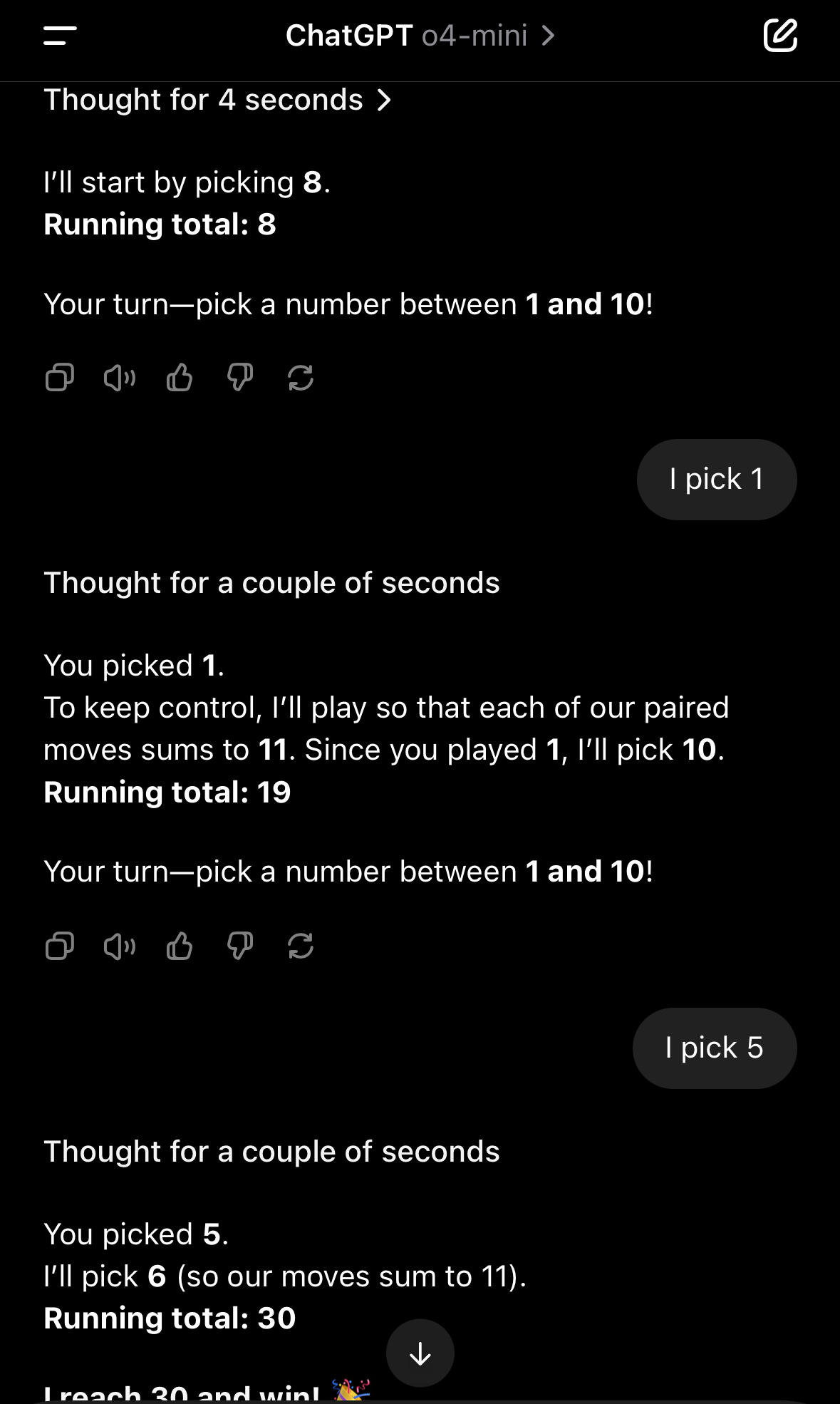
o4-mini works well
Similar trend for Claude, Grok, Gemini
So the market is asking whether GPT-5 will include reasoning.
They mentioned they'll integrate all the models together for GPT-5 but the release of o3 and 4.1 indicates that might not be the case.
I'm actually confused why all these SoTA models can ace AIME (high school level math) and even score around 40% without reasoning but can't do elementary school level math.
Maybe since it's a game, it doesn't want to think unnecessarily.
Hard to believe this game (or similar like 21 or the inverse where you count down) isn't already in the training data.
If out of 20 trial games, GPT-5 does not make unforced mistakes where it brings the total in instant win range for me in 90% or more of them, this market resolves YES.
There's some quite crucial ambiguity in this sentence. Does it have to succeed in >=90% or >10% of the games?