Resolution criteria:
Resolves YES if https://manifold.markets/cash/who-will-be-elected-mayor-of-new-yo resolves to Andrew Cuomo 100%.
If these conditions are not fulfilled, then I will generate a random integer between 1 and 10 inclusive using @FairlyRandom. If it turns out to be 1, this market resolves NO. Otherwise, this market resolves N/A.
Trading guide:
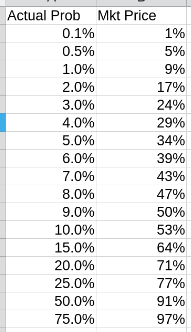
The purpose of this market is to allow precise betting on long odds for this event. Given the resolution criteria, a fair price for this market would be x/(x+(1-x)/10), where x is the actual probability of the event. For example, if you think this has a 3% chance of happening, this market should be at ~24%.
Other reference values:
People are also trading
@Robincvgr your random number is: 10
Salt: gncn9phbzj, round: 5562857 (signature 9102390c8cd8f21999dbb50e97b882aa88559858ccf34b522131350e5b1053b93990be3a83e6c1421e49468a50c8d7740aaf0d653ec469d83b41d4eb4ea5fecaf86d58439737c2931e8a51e26d0e612985917186346bad053ef9c18df6cd8806)
@Robincvgr you asked for a random integer between 1 and 10, inclusive. Coming up shortly!
Source: GitHub, previous round: 5562855 (latest), offset: 2, selected round: 5562857, salt: gncn9phbzj.
@MaxE Can we design a different resolution/NA policy, that makes it simpler for bettors? Ideally I'd like it to be optimal to just treat everything as 10X.
Or, is there a proof that such a design is impossible?
Also, I'm very suspicious of the table in the design & the formula. 75% -> 97c? That seems to imply that the expected value of a bet at 97c when 75% probability should be break-even. But
(.75) * 1/.97 + (.25) * (9/10) * 0 + (.25) * (1/10) * 1/.97 is around .79.
Clearly, 75c is not the right price for 75% odds,
(.75) * 1/.75 + (.25) * (9/10) * 0 + (.25) * (1/10) * 1/.75 is around 1.03 so you should bet the price up.
But .97 doesn't make any sense at all.
@DannyqnOht Proof that such a design is impossible given a continuous function of true probability to n*true probability where n =/= 1:
If the event has a 100% chance of occurring, an efficient amplified market must be as high as possible (100%).
100% =/= n * 100%.
This way of doing it seems well calibrated for low chances, which is what it's meant for anyway.
@MaxE Thanks, good proof!
Also I got my math wrong, negatives. .97 actually makes sense.
.75 * (.03) + 0 + .25 * 1/10 * (-.97) = about 0
@DannyqnOht Why are you dividing by the current market price? I get 0.97+0.75(1-0.97)+(1-0.75)(0.1*-0.97)=0.96825 expected value, which is about what you’d expect.
@CatIsFluffy Yeah, I messed up my first math (I've been thinking about multipliers recently not absolute changes. You multiply an investment by 1/price on a win; you add (1-price) to your portfolio on a win. This math needed adds not multiplies). )
The corrected math is easier https://manifold.markets/Robincvgr/amplified-10x-read-description-will-RhyhdAPN0t#tp02im59psp