https://x.com/mhutter42/status/2001857421569032444
Resolves N/A if the bet is called off. (One party not paying out and the other party magnanimously saying "it's ok, I won't hold you to it" does not count as the bet being called off.)
There will be no AI clarifications added to this market's description.
🏅 Top traders
| # | Trader | Total profit |
|---|---|---|
| 1 | Ṁ19,583 | |
| 2 | Ṁ10,790 | |
| 3 | Ṁ10,644 | |
| 4 | Ṁ10,169 | |
| 5 | Ṁ8,349 |
People are also trading
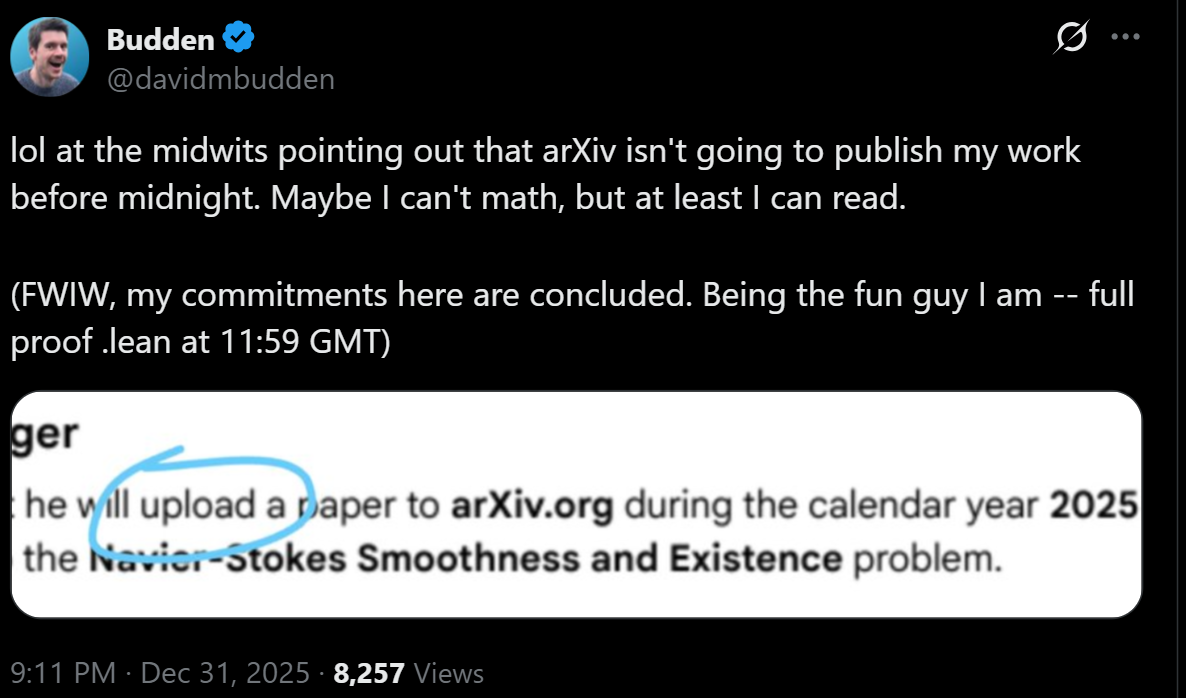
David has conceded, so no need to leave this open for the next two years. Props to @DavidBudden for losing gracefully.
He does still have another month to win his last bet:
@harfe Ill look at this. But please don't create a cascade of ppl sticking the paper in Gemini to get false-negative hallucinations i feel compelled to handle, when they're ironically upholding the stance that the proof cant be right because LLMs hallucinate.
@DavidBudden No Gemini or other AI were used by me here, just beginner stuff for Sobolev spaces (and it would be much easier to check if you were to cite a specific theorem in Evans, not a whole chapter).
@harfe |x|^{-1/4} isn't in H^1 since the derivative isn't square-integrable ,
log log 1/|x| is an example for showing H^1(ball) isn't contained in L^infinity.
(It's also easy to see 2.8 isn't true by considering constant functions f = k)
Kind of surprised this an LLM outputted this tbh it's kind of weird, "there exist universal constants C_1 and C_2" and they aren't like pi/8 or something and you aren't going to tell me what they are? Usually the language at least sounds sorta right before you think about the math.
@NateWatson what makes you think the gradient is not square integrable?
Wikipedia has the same class of examples: https://en.wikipedia.org/wiki/Sobolev_space#Examples
and our case is k=1, n=3, p=2, so for alpha=1/4 the function is in H^1 = W^{1,2}.
@DavidBudden there's some free mana here for you if you want to bet, since you should already know the answer to this one
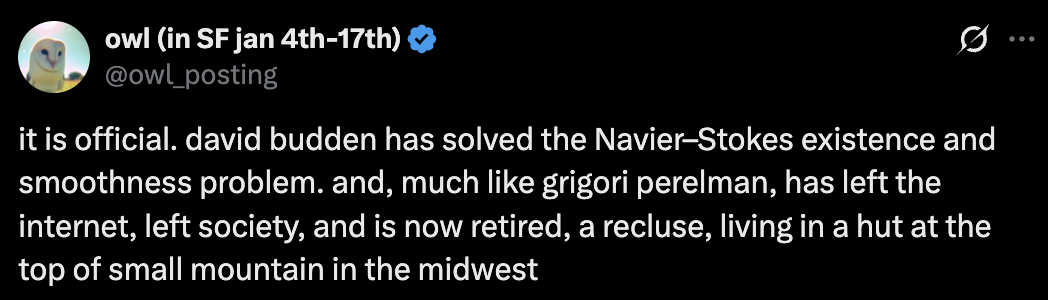
@Simon74fe he solved it but the underground math cabal are silencing him to save face, that's why we haven't heard anything since nye. he knew too much.
@retr0id I guess that's what we can derive from this volume of information - an area of expertise integral to his absence
https://arxiv.org/localtime - I'm not terribly familiar with the arxiv process, but assuming the paper was submitted before EOY, my understanding is that we should expect to see it by Jan 5th 01:00 UTC
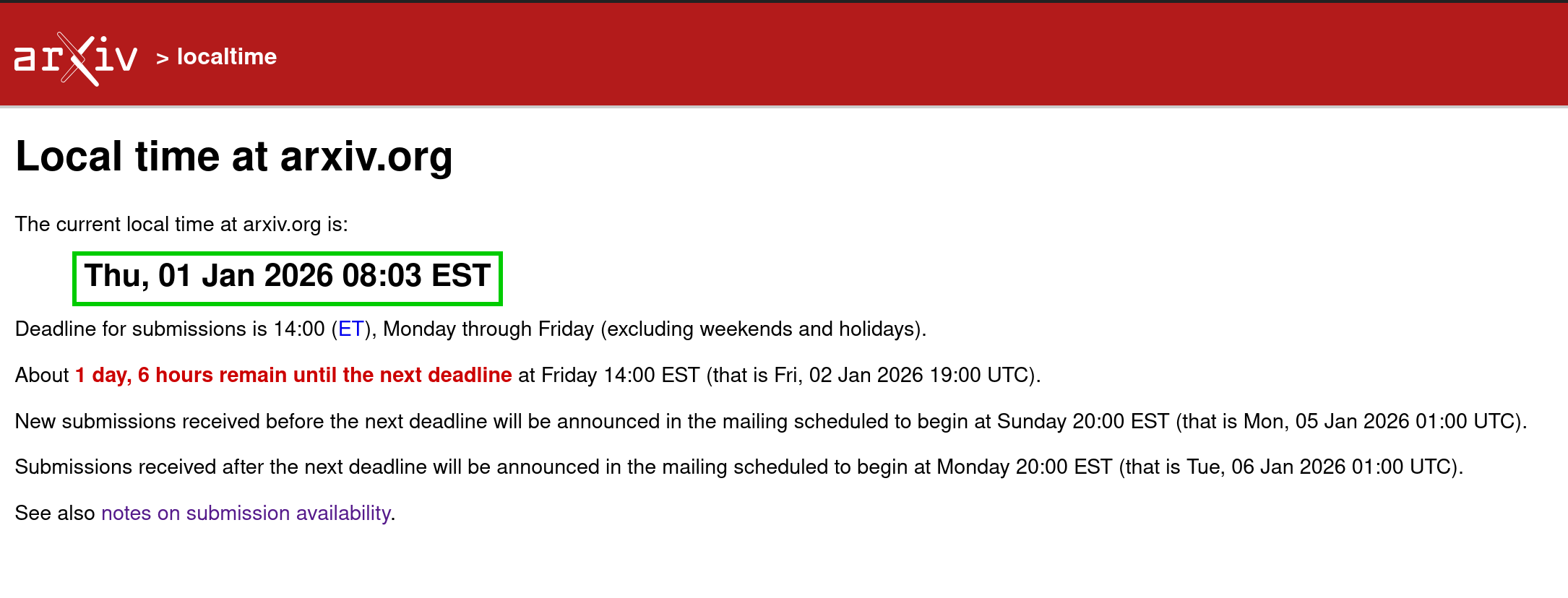
I assume that the market resolves yes if he doesn't upload a paper purporting to contain a full proof by midnight UTC+0, which has elapsed?
@ArnavRawat The original bet didn't specify a time zone, so personally I think the terms would be satisfied if David uploads it before the year is out in any time zone. (Of course, I am not the arbiter of the original bet, Marcus and David may disagree.)
l
@retr0id I could totally be wrong, but I'd be surprised if any of these tiny timing details ended up mattering. My actual guess is that if David Budden tweets the Lean file out a few hours after midnight, and then uploaded a paper to arxiv tomorrow or the day after, and the Clay institute accepted it, then probably Hutter would just concede the bet. I could be wrong, I don't know Hutter, but I think it would be a very reasonable choice to be like "the real thing I was wildly skeptical of is if you'll prove it this year, and you actually did". (But Hutter sticking to the text as written would also be reasonable, to be clear, I just don't expect it.)
@PeterSchmidtNielsen yeah I can imagine there being some leeway if he's actually solved it. although at this point it just looks like he's going to stall indefinitely
@retr0id yeah, solving it is the hard part. If it's close enough for us to be quibbling over time zones, and it's actually solved I'm not mad if it resolves that way.