🏅 Top traders

And now trending on Reddit

https://www.reddit.com/r/todayilearned/comments/12t2d7z/til_that_69_number_is_the_only_natural_number

A massimo retweet, nice!

https://twitter.com/Rainmaker1973/status/1649060100802330625?s=20

The time is almost here folks! To see whether anyone’s been hoarding a nice number waiting for March 31.

@JoshuaB Implying I only found one 😏

@JoshuaB Nah, no one has a large enough YES position. They'd have placed a limit order around 5%.

@IsaacKing There’s a bloody lot of liquidity to make still. For only 600 mana they could make 6000! (Though I don’t disagree it would’ve been more profitable to have a limit order)

I feel maybe one direction we haven't looked at is the multiplicative group.

For a prime base p if we look at the k last digits of a number we get a member of Z/p^kZ.

Now if the order of that number is too low it is more likely for these last k digits to repeat in powers of it.

This search for "nice numbers" kinda reminds me of the search for extraterrestrial life. I've been pretty adamant that all life is from earth since there are more ways to shuffle a deck of cards than atoms in the universe even though most people think it's all but guaranteed that life isn't an anthropogenic concept (made by humans) due to the vastness of the universe. This is analogous to the view that 69 base 10 is the only nice number since it was discovered because humans like base 10 and the number 69 and doing math and there is no sign of any other nice numbers other than the shear amount of numbers that exist.

I am quite sure it is easily provable that besides the b-1, there's no further information to be gained from any remainder of the sqube.

For example try calculating modulus 99 for some 1234567890 in some permutations in base 10. You'll notice you get exactly the same amount of information as modulus 9.

Perhaps that is too far, but it feels so hard to find such things.

Grant Sanderson wrote back to my email! He said he didn’t have any ideas, but he would give it more consideration once finished with his current project, and consider it as a potential future video topic.

@Conflux

Here's how to make real progress on the problem. Since (n+k)^2 = n^2 + 2kn + k^2, then for base 120 and a range of say k=120^4, we have ~48 total digits; ~20 of these remain the same, ~20 change with the 2kn term (they basically change linearly) and only 8 are affected by the k^2 term. Around 40/48 digits of the square and 40/60 digits of the cube can be approximated linearly, and each digit tracked narrows down the search space by more than the previous digit.

There is a similar problem on mathoverflow which can be solved with lattice algorithms despite naively having an exponential search space. I can't find a way to easily adapt it to this case, but maybe someone could.

@ThomasKwa There are two problems with adapting lattice algorithms:

• "all digits are distinct" is harder to express in a polynomial than "all digits fall within predefined values"

• In the mathoverflow question the constraints are all modulo p, whereas here the modulus might as well be irrational

Nevertheless there's enough structure here that the problem seems solvable in theory.

About the first part, we could maybe start by demanding the sum and product of digits to be correct. I am not certain this is enough to make it unique. It probably isn't if you must add some modulus.

However there are other functions which do not depend on order. You could for example square all digits and sum them. Any power would work I think if we need even more constraints.

Squaring and multiplying them isn't going to be useful because it contains no kore information than just multiplying them.

We do not have to embed the problem directly in a polynomial, any sufficiently constrained system would do.

Another kind of such function would be to add something to all digits before multiplying them.

Or we could another route, the determinant for example is always zero if it has non distinct arguments.

I think all big multiplications and divisions can be eliminated, including base conversion. You can store the digits of n, n^2 and n^3 already in base b, then compute the next n, n^2 and n^3 using additions only. My guess is this is about a 10x speedup if implemented well. It should also work with the mod b-1 observation, you just need to also store 2 (b-1) n and such.

Also building the set of digits every time is unnecessary since the first ~b/5 digits of square and cube remain the same.

@ThomasKwa Oh that’s really smart! Seems obvious in retrospect to try.

Perhaps I was behaving a bit too much like the person who wanted to close the patent office in the 1940s or something because there was nothing left to be invented, since it seems like people are still finding insights on this problem that seem pretty canonical. I’m still skeptical that we can really get anywhere, but maybe if we knock off a few more orders of magnitude we’ll have a chance!

@ThomasKwa you're still looking for a needle in a 120^120 haystack. Constant factor speedups won't help.

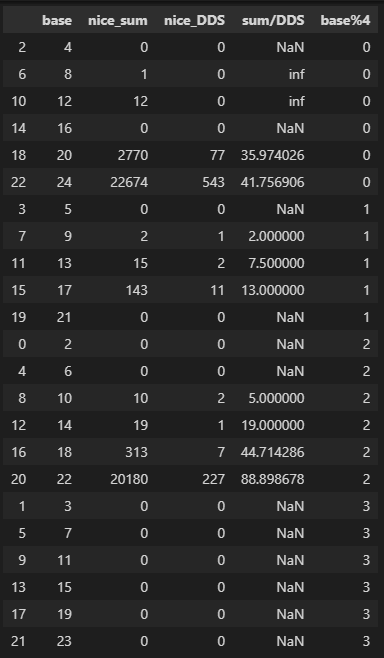
Hmm I noticed an odd pattern.

Since checking the digits sum (DS) of the sqube turned out to be useful, I tried finding all the numbers with the right digits square sum (DSS).

First thing I noticed is that while yielding far less results, like with DS, no numbers with nice DSS were found in bases that are 3 mod 4.

That prompted to look for other patterns in mod 4 and I found this: I divided the amount of numbers with nice DS, by the amount of numbers with nice DSS in each base.

It is strictly increasing only when filtering by b mod 4.

I wonder if bases with a certain mod 4 are more likely to have nice numbers and if we can extract some optimization out of this.

here is ordered by base%4, look at sum/DDS collumn:

and here is only ordered by base:

note by the way there's a formula for 1^2+2^2+3^2+4^2... https://en.wikipedia.org/wiki/Square_pyramidal_number

@NoamY Ooh interesting angle! Yes, 3 mod 4 is proven to be impossible. Proof is in my second blog post - the reason is that it can never have the correct remainder mod b-1.

Yes, I read your blog posts:)

What I'm wondering is is there more to mod 4 than that?

@NoamY Oops, sorry for not really reading. I'll try to take a more in-depth look at your results later!

@NoamY Alright, I actually read your comments. Sorry. The mod 4 increasing pattern seems pretty interesting! It seems very plausible that the different square-sum residues mod 4 would have different densities of nice numbers, since if I recall correctly, this is true for sums. I am curious, do square-sums have any nice mathematical properties like regular digit sums? Do they have to be conserved in a modulus? They might be but I can’t quite convince myself at the moment.

I can't find any useful property of digits squares sum. I looked at OEIS and didn't anything useful either.

I tried replicating this behavior with the quasi version with success.

I also noticed the same thing when sorting by b/4 for both quasi and non quasi.

This implies it's a function of b/4 and b%4.

I'm afraid I'll have to start optimizing though if I want to collect more data. Maybe even move to c++. Do you happen to have the c++ code that guy who searched around base 40 wrote?

@NoamY Nope, I’ve got Python code but I’m afraid the person who said that is just “some guy on reddit”