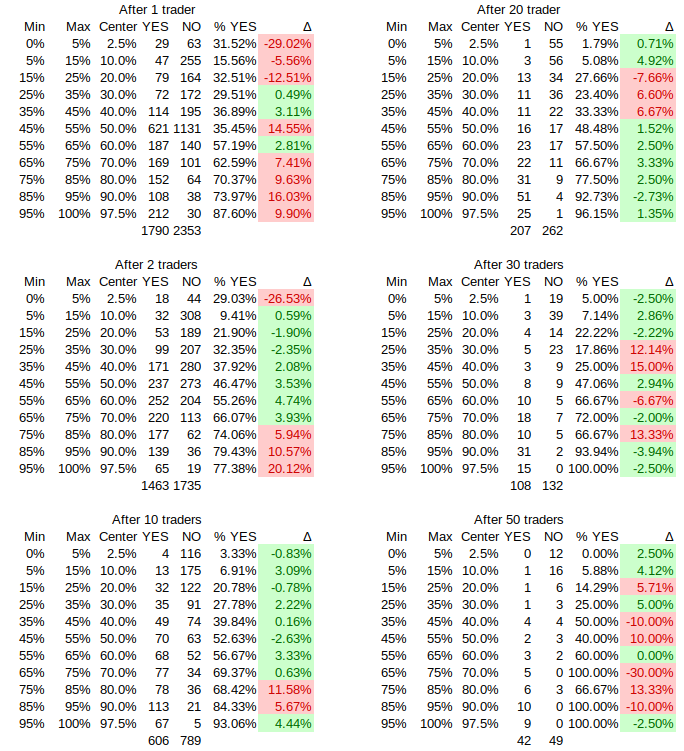
Explanation of the analysis:
Consider all resolved, binary markets (binary just because I'm being lazy about handling free response markets). Now consider the market probability after the first unique trader, the second trader, and so on. When considering the n-th trader scenario, we exclude any markets with fewer than n traders entirely.
Manifold is, overall, well-calibrated, and it is probably the case that adding more unique traders increases accuracy. So: going through the procedure above, what's the smallest value of n where Manifold will be well-calibrated?
For the purposes of this market, "well-calibrated" means that when I bucket predictions around 2.5%, 10%, 20%, ..., 90%, 97.%, at least 7 of the 11 buckets will be within 5 percentage points of perfect calibration.
If you would like to see how everything is calculated my code is/will be here: https://github.com/vluzko/manifoldpy
🏅 Top traders
| # | Name | Total profit |
|---|---|---|
| 1 | Ṁ231 | |
| 2 | Ṁ65 |
People are also trading
If anyone would like to check the code it is here: https://github.com/vluzko/manifoldpy/blob/main/scripts/num_trader_calibration.py
They're not well-calibrated at start: older markets could start with non 50/50 probabilities, and this is still available through the API.
Honestly I just don't really care about Brier score. Proper scoring rules are nice but they don't really give you any insight into how to update given a predictor's output.
@vluzko Point taken, the answer is not 0. But I expect it to be very small (possibly even 1). Calibration is necessary for a good market but not sufficient.