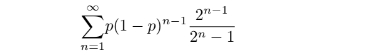Background: The snake eyes paradox market.
Algorithm description:
We start with 3 people willing to play the gruesome snake eyes game. First 1 person will be chosen at random for the initial 1-person group. If that person survives (rolls non-snake-eyes) then we choose the remaining 2 people for the second group and roll for them. You only die by rolling snake eyes.
We repeat the above a [million] times. Each time, we record who was chosen and who died. We then count how many of the [million] times person 1 (WLOG) was chosen to play. (Again, that happens either when person 1 is chosen first, with probability 1/3, or when whoever was chosen first survives.) Call that count C. Finally, we count the number of times, D, that person 1 died.
Output D/C.
🏅 Top traders
| # | Trader | Total profit |
|---|---|---|
| 1 | Ṁ29 | |
| 2 | Ṁ22 | |
| 3 | Ṁ9 | |
| 4 | Ṁ8 | |
| 5 | Ṁ6 |
People are also trading
Voila! I wrote the code:
trial[] := Module[{pop, g1, roll1, g2, roll2},
pop = {1, 2, 3}; (* three people in the pool *)
g1 = RandomSample[pop, 1]; (* pick group 1 *)
If[g1 == {1}, chosen++]; (* focus on person 1 WLOG *)
roll1 = RandomInteger[{1, 36}]; (* take 1 to be snake eyes *)
If[g1 == {1} && roll1 == 1, dead++]; (* snake eyes *)
If[g1 != {1} && roll1 != 1, (* person 1 in round 2 *)
g2 = Complement[pop, g1]; (* group 2 is everyone else *)
roll2 = RandomInteger[{1, 36}]; (* 2nd dice roll *)
If[MemberQ[g2, 1], chosen++]; (* always true w/ 2 rounds *)
If[roll2 == 1, dead++]]; (* second roll *)
dead/chosen];And here it is converging neatly to 1/36 over 10,000 trials:
@dreev the approach of having a set in memory for the pool of people will not allow you to use the same program and increase the set.
How would you hold a set of 10^100 members? My point is, you cannot learn with this program how the function would behave with increasing pool, but isn't it what you wanted to achieve finally?
@KongoLandwalker Do you want to preregister a prediction for what this code will output as we increase the number of rounds from the current 2? We can't get to 10^100 but we can get to, say, 100.
@dreev in my attempts the 1/36 started to slowly converge into .5 after the limiting amount of people was set to 10^27 or even higher I think.
I was limiting by people in the recent Python code, but now you are limiting by rounds... strange that you start to cap by a new thing. Just a bit inconsistent.
Anyway, hitting 100 rounds is not an unlikely event.
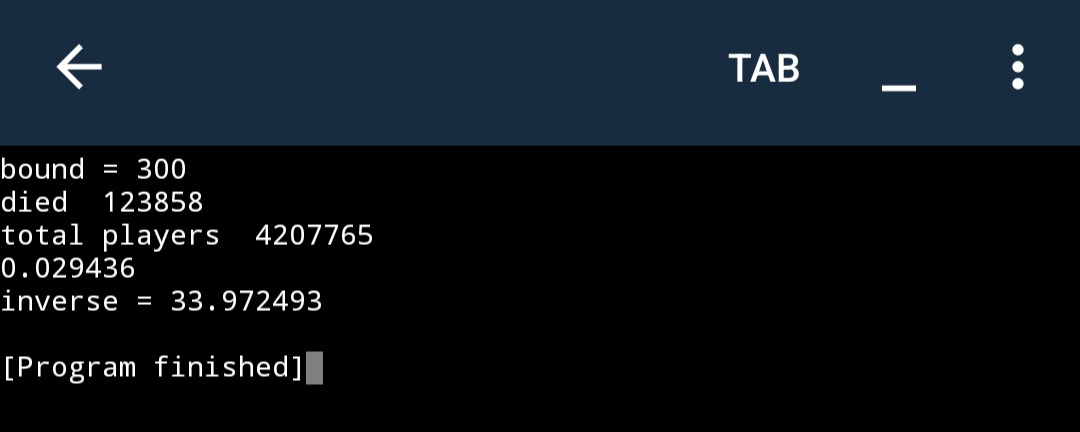
100 rounds gives around 1/35.6
9999 rounds gives 0.5
@KongoLandwalker Limiting by population or by number of rounds is the same thing if we pick a population size that's one less than a power of 2. That's why I have a population of 3 in this 2-round version. But, as you say, that's not central to the debate.
Just to make sure, we're talking about the finite version of the game in which, when we run out of people or hit the max number of rounds, no one dies? (I.e., only ever killing people based on a fair dice roll.)
we're talking about the finite version of the game in which, when we run out of people or hit the max number of rounds, no one dies? (I.e., only ever killing people based on a fair dice roll.)
Yes. if you set round_limit to 100 you are still getting 1/36 or 1/35.
if you make round_limit to 9999 you will get 0.5
9999 is higher, so it is closer to representing "unbounded game".
It is easy to make not bounded games. Just let the code run until snake eyes in While loop. Due to (35/36)^n exponentially dropping, you are guaranteed to successfully meet the snake eyes.
@KongoLandwalker Progress! Thanks! So you claim the probability stays very near 1/36 when n is as high as 100 but but as n gets into the thousands, the probability gets closer to 1/2? Can we find an analytical expression for that exact probability in terms of n?
(This is exactly the process I went through originally, btw. It wasn't remotely obvious to me before doing a lot of math.)
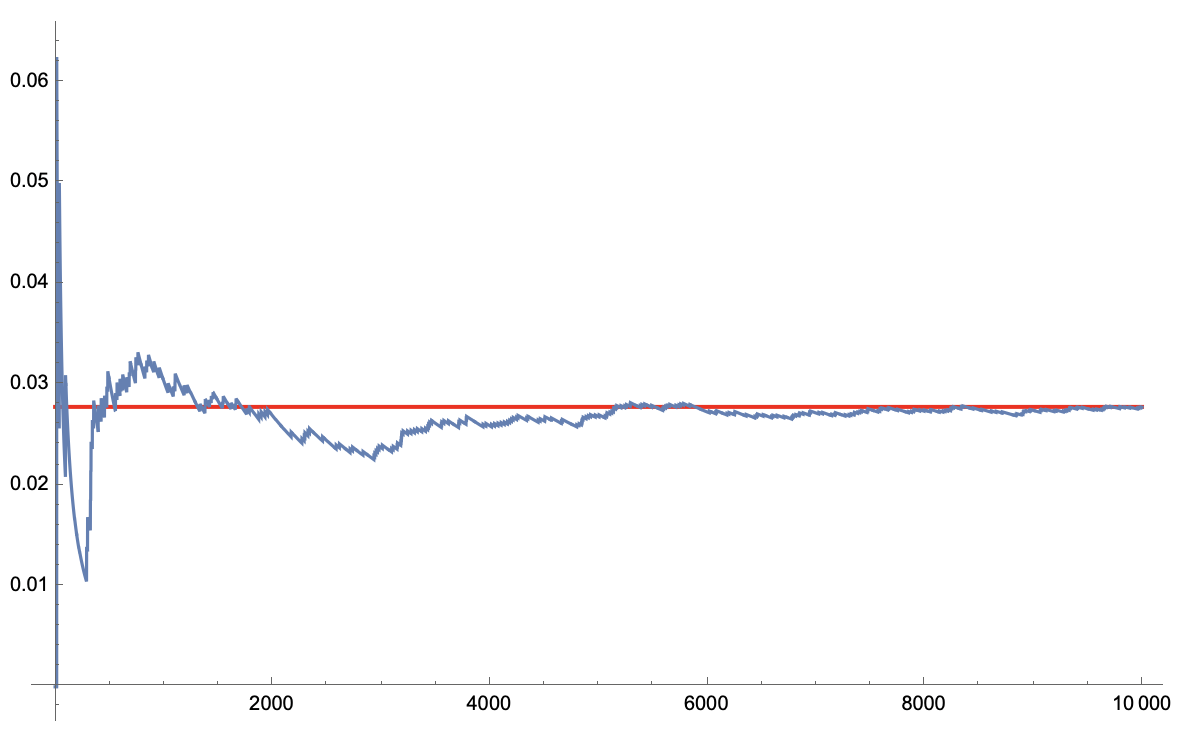
@KongoLandwalker for $m$ rounds, to achieve a successful trial detection rate of $r$ of a maximal round case you would need $Log (1-r) / Log (1-(1-p)^m))$ number of trials. So setting $m$ = 9999 requires some astronomical number of trials that you are unlikely to be able to run on a computer. Excel cant even compute the number of trials necessary for $m$ much greater than 1328. I am not surprised that for large $m$ you sample trial size is not detecting any maximal rounds.
@Primer Wait, why did you give me a 2-star review on this market? Did you want to see a graph with literally a million trials? (To be clear, it converged fine within 10k trials.)
@dreev I thought this would resolve to the stated criteria, yes.
Star ratings are new and it's not easy to rate consistently as there is sampling bias: How many really bad markets does one participate in?
I really like Metaculus' standard concerning resolution and would love to see the same here. On reflection, that doesn't seem feasible here (yet).
Revised to 3 stars. The market assumes a particular interpretation of the parent market which is debated and thus will be misleading when taken out of the context of the parent's ~1k comment discussion. Also it just didn't resolve to the stated criteria.
@Primer I humbly present you with the million-trial version:
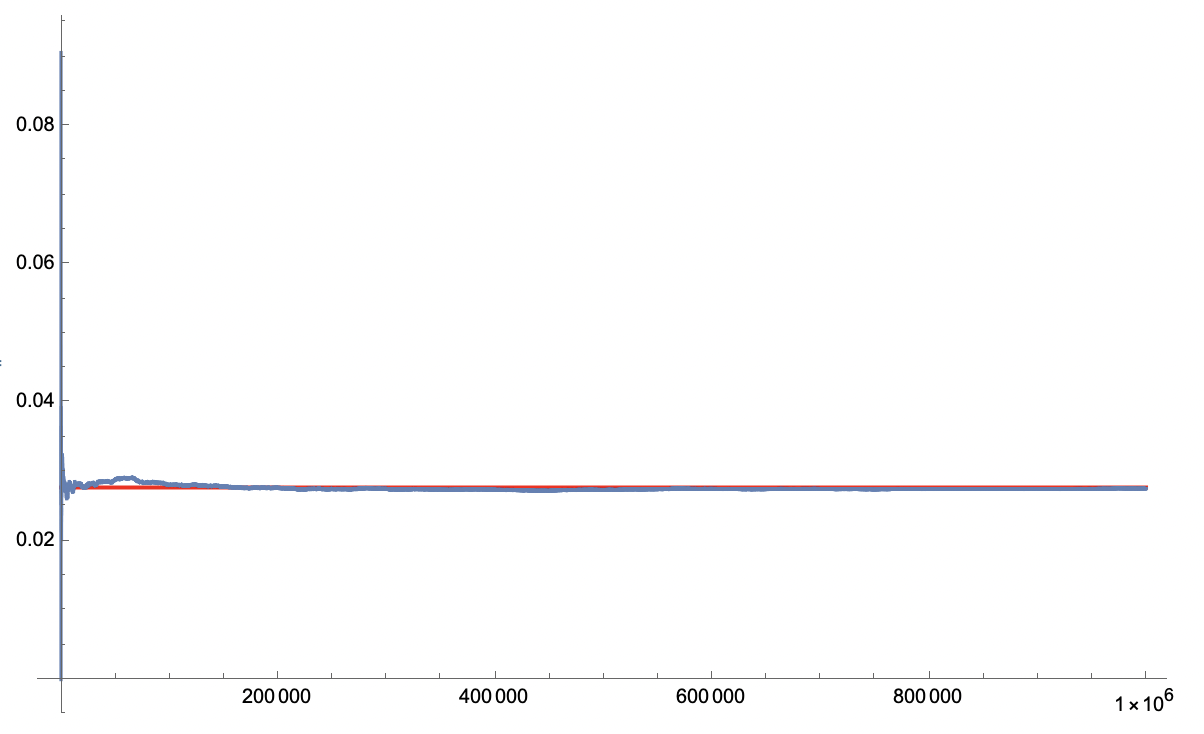
(It's already converged so early it's hard to see, which is why I displayed the 10k version before.)
As for the implications for the parent market, that's what I'm working my butt off to clarify with these child markets. Did the code I wrote for this one not match the algorithm in the description? I probably deserve 1 star for the mess I made in the parent market -- failing to anticipate various ambiguities -- but I don't understand what's wrong with this one. The result of this simulation, before I worked out the math for it, was a huge surprise to me and was key in convincing me personally that the answer to the parent market is 1/36. Others aren't convinced but I think it was valuable to get on the same page about this particular subquestion. Maybe you'll say it's all misleading in the context of the parent market because there's a different, better subquestion with a different answer. If so, let's get that subquestion asked as well!
@dreev You really didn't have to run the million trials now, everyone believes it's 1/36. I have no reason to doubt that your code matches the description.
The thing is: Someone not willing to read through >1k comments will read those question titles and assume there is consensus the parent would resolve to 1/36 in the 2-round szenario as well.
If you wanted to point to possible agreements (or clarifying disagreements), you could have made the equivalent question for the other side as well, using the same title. Or you could have just called this one an "interpretation of Snake Eyes" or some other different name.
@Primer I see. How about the edit I just made to the title of this market? Does that address the concern? I'm still interested in other interpretations of two-round versions of the snake eyes paradox. Part of my point in all this is that those other versions do not make sense or deviate pretty starkly from the original description, eg killing the final group regardless of the dice roll. But that's the ongoing debate.
Does that address the concern?
Yeah, absolutely! That change is very welcome!
I'm still interested in other interpretations of two-round versions of the snake eyes paradox
Same as this market, except only games actually ending in snake eyes count as playing Snake Eyes.
Of course this has 1/36. You introduced a possibility for the game to end NOT BY snake eyes. It is not equivalent to the original problem, where it ends IF AND ONLY IF snake eyes.
I see this market as another attempt to manipulate not attentive people into thinking your position is right.
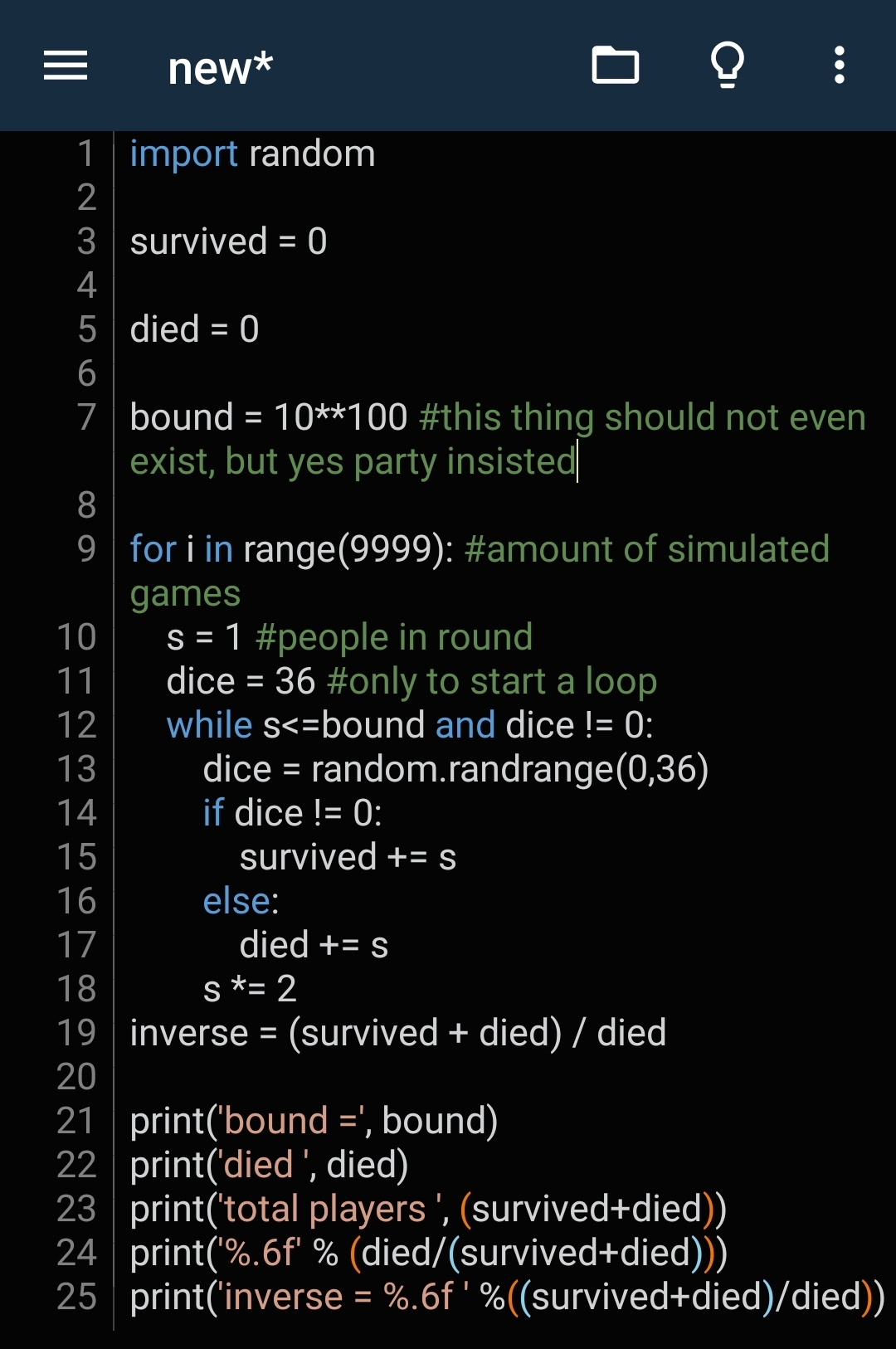
Now carefully watch what happens if the bound is set not to 3, but to actually high number.
If there were no bound, that would be the same as having bound = inf (like in proper snake eyes), so any finite s < inf is true.



@KongoLandwalker, I was gong to counter, but fuck I can't keep up with this moving target:
> The question is about the unrealistic case of an unbounded number of people but we can cap it and say that if no one has died after N rounds then the game ends and no one dies. We just need to then find the limit as N goes to infinity, in which case the probability that no one dies goes to zero. [ANTI-EDIT: This is back to its original form since a couple people had concerns about whether my attempts to clarify actually changed the question. A previous edit called the answer "technically undefined" in the infinite case, which I still believe is true. The other edit removed the part about how the probability of no one dying goes to zero. That was because I noticed it was redundant with item 5 below.]
(from https://manifold.markets/dreev/is-the-probability-of-dying-in-the)
So is this program evidence that the ~0.521887 summation is flawed?
No, the mathematical approach is more accurate.
Mathematical summation is perfectly weighted, but in simulation the game is not running long enough (and never will) to weight every case the same AND there is a key difference in the approaches. Mathematical calculates the weighted sum of deathrates. Simulation calculates deaths/all (and this approach was suggested by YES party member).
In general a/b + c/d + e/f != (a+b+c)/(b+d+f), and that is why simulation gives another answer.
Left part is analogous to mathematical approach and the right one to simulation which I have done.
My point is to show, that both of those give NOT 1/36, even the simulation, code for which was written by @JonathanRay I think . I only raised the bound from something like 2^20 to 10^100.
The whole result of the simulation gives around 1/36 in low values of bound, but as bound increases, the result of a simulation grows up to 0.5.
By the Snake eyes market statement, we are interested not in low bound numbers, but in infinitely high bound numbers (unlimited pool).
In the program if you straight up delete the bound and allow each game be simulated to its finish, then you get 0.5
@KongoLandwalker the 1/36 only arises only if there are games which don't roll snake eyes, either because you ran out of new people to play with or because you have games that can last infinitely long. In simulation the game is not running long enough (and never will) to simulate an infinitely long game.
@ShitakiIntaki that is one of the reasons why mathematical approach is even more accurate.
What will be the ignored addend in the infinite sum, you will ask? The case where the game is infinite.
Let's compose it the same way as all other parts.
Instead of a probability of "a game which finished in round N" p(1-p)^(n-1) we will have lim[n->inf]((1-p)^n). Because that is the probability of the infinite game.
Instead of (2^(n-1))/(2^n-1) (the rate of deaths in the game which wnded in round n) we will have 0, because no one dies in the infinite case.
So now we have to add this to the 0.521887.
Σ(from all finite cases) + infinite case = 0.521887 + (inf small number) * 0 = 0.521887
but we can cap it and say that if no one has died after N rounds then the game ends
He corrected again but still did not Touch the Problematic part.
In general a/b + c/d + e/f != (a+b+c)/(b+d+f), which is why you cannot piecemeal over different conditional probabilities and reassemble them by a summation. They all have a different denominator, you need to get back to a common denominator by having a common conditional event.
@KongoLandwalker Here are my computed maximum bound $m$ for which a scant 9999 trials can successfully detect at least one maximal round trial. As posted else where you will need exponentially more trials to detect the increasingly rare maximum round case, but you held the number of trials constant as you increased the bound, so each time your were effectively exponentially under-sampling.