🏅 Top traders

(deleted)

Anyone up for some more randomized fun?

https://manifold.markets/BenjaminShindel/which-set-of-words-is-random?r=QmVuamFtaW5TaGluZGVs

Which set of words is random?

50% chance. I used https://randomwordgenerator.com/ to generate 3 random words. I used the first three words I generated. I then came up with three words on my own, after seeing the first set of words. I did not use any randomized method for selecting my set of words. I used an online coin flip to assign the order of the two sets of words. Bet for the set of words that you believe to be the RANDOM set. (if you think the "YES" set of words is randomly generated, bet "YES", if you think the "NO" set of words is randomly generated, bet "NO". I will obviously not bet in this market. I took a picture of the random word generator that will have a time stamp on my iphone. If people like this market, I will iterate on it and make more exciting/strategically interesting versions :) YES: consideration gossip orchestra NO: fervent production rhyme

I am doing post mortem on my chi-square test. The main result I considered was obtained using 80 points. The source code is here: https://pastebin.com/n56c80fA

Results:
P-value green: 0.0116

P-value red: 0.2757

P-value green: 0.0909

P-value red: 0.8942

Now, I used the generator published by @Loppukilpailija to generate 80 points many times, reconstructing the histogram of p-values for middle digit and last digit.

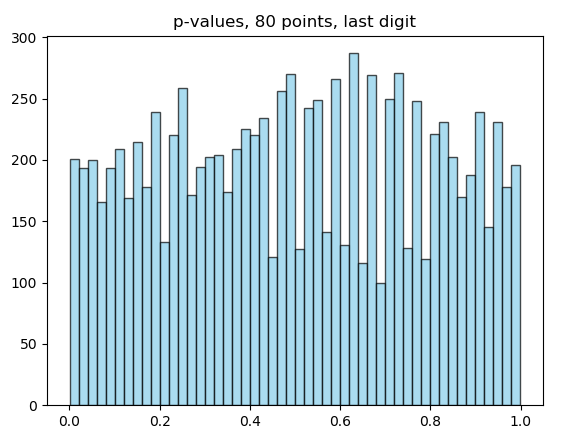
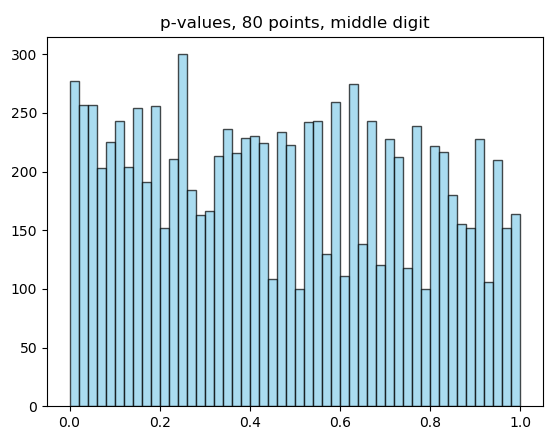
So, I am still confused. I would have to be extremely unlucky for the test fail as it did. The source code to the histograms, including the random generator I copied in, can be found here: https://pastebin.com/zR5wpkBd

Just to be clear: The histograms of the single-digits are not random uniform, there are mild differences (I can past the histograms, calculation is included in the code). But 80 points repeatedly produce almost evenly distributed p-values, so the difference is probably not detectable on 80 points.

P.S. Yes, the code is stupidly ineffective, I was lazy to polish it.

I warned ya’ll ChatGPT said red. They call him “Advanced Data Analysis” for a reason.

@Tux him?

Fantastic market @Loppukilpailija. Was a lot of fun.

I got eaten up by this market because I was underconfident and thought that others had more knowledge than me. Lucky to still come out with a profit. Was generally confused and still am.

I struggled between the arguments that easy human-generated errors like average distance, angles, and quadrant flips all pointed to RED, while GREEN was far too clumpy and RED look very random on many metrics

@PC I think the tale of this market was not that anyone should have been more confident.

To make money here, you should have been less confident. We just didn’t have enough evidence to support either YES or NO with high confidence.

For example, my private estimate was 51% for YES. What I should have done is buy NO when the market was above 90% YES, not because I thought the outcome would be NO, but because I estimated a 49% chance of NO and buying NO was cheap.

Anyone who spent a very large fraction of their bankroll here was overconfident. Even if they bet correctly on NO. Because about half the time they’d had lost.

I am glad that this market bet so strongly against the actual outcome. This way one can feel the overconfidence and the associated loss. If the market had resolved YES instead, it would have been harder to recognise the mistake, given that one has won.

Can I suggest a banner image for this market?

All of my point! Lost!

Very nice markets, big thanks to OP

@CamillePerrin I’m rooting for your epic comeback.

Thank you @Loppukilpailija for this great game! I learned something, and following the comments was a lot of fun.

This market is a cautionary tale about pareidolia and what happens when you over-rely on p-values.

when you over-rely on p-values.

I don't think p-values are the specific issue? Just over-relying on methods of analysis you don't necessarily understand? "likelihood that the null hypothesis distribution would produce a sample with a property greater than or equal to this" is a reasonable thing to look at here, right?

@jacksonpolack I'm not sure it is, it makes you very vulnerable to accidental p-hacking when throwing properties at the wall and trying to get one to stick, with no preregistration and pretty much zero clues as to what properties have a high chance of actually being correlated

That's just 'running multiple tests and believing in the result if only one is positive', which can happen with or without p-values

How it went for me: I was very enthusiastic about the market from the start, but I had the uneasy feeling "I hope OP didn't go overboard with the secret transformation stuff, they may just render a ton of work completely worthless". I tried lots and lots of statistics and became convinced green was a way to go. Then at about 80 points it all collapsed, also OP revealed that yes, everything I was trying was in fact bullshit. I was left in a state of total doubt, sold all my green and bought 20 red thinking that I no longer had any idea what was going on, but the market was probably overconfident. I made some profit, but it's clear I'm not good enough at stats to have solved it. Not sure if anybody got this one right in a rigorous, principled way, but if you did, wow, you have my respect.

@Tasty_Y Maybe someone who was not betting a lot or engaging with the comments knew something that we didn't, but I don't think myself, Phil, or Capy really knew what was going on. Even if I ended up being right, my reasoning was all wrong.

@Shump I know you just don’t believe me, but I think the knowledge that one set had a transform that added radial-only spread was critical information that could be used.

@capybara Great job! Can you share more? I couldn’t figure it out myself. Got scared that Shump was selling

@capybara I tried to convince ppl in the comments below. If it doesn’t make sense, I can try again.

@capybara by spread do you variance of spread?

@Shump I actually wonder why you sold. I imagine it was because you did the analysis of distance from the middle. I think your reasoning was sound.

@PC Each point gets sent to one of 8 positions, but all 8 positions are roughly the same at distance from (300,300) for each point. So by spread I mean spread around at whatever radial distance they started.

Yes, and at the set level, what metrics change? A uniform set will likely still have the same spread?

@PC For example, distance to neighbor. Points near (300,300) effectively won’t move. Points far from (300,300) will move a lot. Areas with few points but away from (300,300) are more likely to get a point move into it than an area with few points near (300,300). For example.

Importantly, the transform is idempotent statistical, so that we can apply it again, and metrics are more likely to change if the transform has not been applied already.

@PC I left a comment in a thread below but my reasoning is that basically, if we apply the transformations again to each dataset, if the difference in metrics is real then you would expect the difference to remain, but if it's a fluke you will see regression to the mean. All of the indicators for red failed on this test, so I was left with no argument for red, and still several for green. The distance from the middle is one thing but some other metrics that indicate green also seem to be resistant to the transformation.

@Shump Did you test it on angle sharpness?

@capybara That doesn't sound right: the OPtransform is only erasing information, it can't introduce any noticeably abnormalities. It's not going to make things randomer than random, or more evenly spread than random in any way. A uniformly random set of points to which OPtransform was applies would be indistinguishable from another random one.

@PC Yes. All of my indicators relied on order. Reshuffle the dataset, and they become insignificant. Some green indicators like discrepancy also fail the analogous test for the other transformations, but not all.

@Shump oh wild, I just tested it. It looks like you are right

@PC so it might have been luck. But the distribution of potential values for RED is more extreme, and it happened that the transformation created one that was extreme

sample 2 points from uniform in 389x389 square. And run the following test: are two points within a 10x10 test square. The probability is uniform over larger square. Now sample 2 points and apply transform. The probability of both points being within test square is now higher near the center compared to far from center.

@capybara Finally, sample 2 points and run transform twice. Nothing changes from the situation where you applied it just once.

@capybara What 10x10 square, any square? Why 2 points and not 1?

it’s just an example. I chose two points as it’s simple and still works. I chose 10x10 but any size should work as long as it’s not like 398x398.

@capybara 1 point is simpler than 2, will your idea work with 1 point? 10x10 positioned however I want?

@Tasty_Y Because the quality that chances is point density. It changes differently according to distance from centre.

@capybara This has already been said, but the uniform random distribution, with the transformations applied to it, is still the uniform random distribution. Point density doesn't change. That's because for every point, there are 8 points that can be mapped to it after transformation, each with 1/8 chance. If you're getting anything different you might have a bug.

@capybara Do I understand the test you are proposing right?
Generate 2 points. Notice how often both end up in a 10x10 square, call this P1.

Generate 2 points and apply the transform, see how often both end up in the same 10x10 square, call it P2.

And the claim is that P1!=P2? Is that right?

@Shump Yes, but 100 points sampled from uniform distribution is it’s own thing.

Example: expected neighbor distance differs for 50 vs 100 point samples. So clearly there are properties of 100 point samples that are not properties of the uniform distribution.

@Tasty_Y Yes. Choose an test location that’s away from centre for maximum effect, or just average over all possible locations of 10x10 box.

@capybara I went ahead, did the test as described and P1 and P2 became equal with enough trials, as was expected. I think you are very much mistaken, feel free to write some simulations for yourself and see.

can you try with more than 2.

@capybara No my man, you write that code.

Alright, will to tomorrow. Just thought you would just have to increment a variable.

@capybara it should be equal if you perform this experiment many times, because you are not changing the distribution.

@Shump I think that is this might be the point. I believe that the average is the same across many tests, but the variance increases

I tried a few metrics and couldn't find any evidence to support the idea about radial spread and the box test, so that looks to be false intuition!

Having said that, I would like to present an alternative perspective. What is useful to do when you know the transforms have been applied is to realise that from the single given rand_transform(human) we can compute all possible transformed point sets. No single one is better, and given that we can, we should consider all of them instead of just the one we are given. Below is the scipy.discrepancy for 10k random samples (blue), 10k transforms of reds (orange) and 10k transforms of greens (light green). The original red and green discrepancy are the dashed red and green lines.

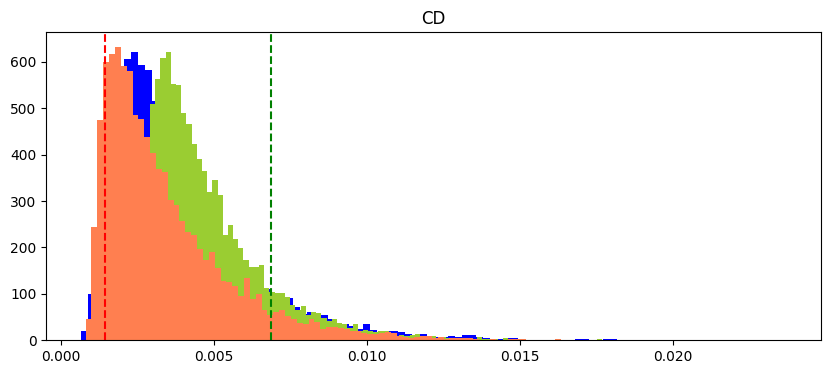
You should do this so as it is free information as to whether the single given human generated sample has had an unlikely transform.

With this, I think a lot of metics that are 9/1 in favour of green being human will regress to say 6/5. In the end, this idea can't be used to favour No, but it can certainly be used as an argument as to why odds should be less than say 70% Yes.

So I think there was a signal to which I was ascribing a very wrong interpretation, and @Shump's argument about regression to the mean is probably a better line of intuition.