At the conclusion of this market, I will resolve the market to the integer nearest 2/3 of the average of all yes shares held.
I will use standard rounding, e.g. 10.5 rounds to 11, 10.49 rounds to 10.
Average of yes shares held is based on yes shares held in each number. So if at market conclusion, there are 100 yes shares for "50" and 100 yes shares for "20", the average is 35. Similarly, if at market conclusion 100 yes shares are held at "50" and 50 yes shares held at "20", the average is 30.
2/3 of the average will be calculated as the average * (2/3). So if 100 yes shares are held at "50", and 50 yes shares held at "20" then the average is 30. 2/3 of 30 is 20. The market will resolve to 20.
🏅 Top traders
| # | Name | Total profit |
|---|---|---|
| 1 | Ṁ3,508 | |
| 2 | Ṁ1,187 | |
| 3 | Ṁ323 | |
| 4 | Ṁ204 | |
| 5 | Ṁ37 |
People are also trading
I created a simple website that allows you to click a button to run a script that spits out the current YES shares for every answer, as well as the weighted average and expected resolution.
https://houstoneuler.pythonanywhere.com/
Some of my previous trades took more than 10 minutes to reflect in the data, so the results might be delayed.
I have once again manipulated the market (legally), and written a post about my actions: https://houstoneuler.com/2024/02/08/manipulating-markets/
I wrote another post about this market, with an update on the current expected resolution in Green. Curious to see how this chart evolves over time.
@houstonEuler good read, thanks for posting. Don't be offended that I bet against you in your blog everyday market. FWIW, this market is probably not as interesting if the volume doesn't materialize. Marketing it is much more difficult than I anticipated.
@Jerkstore Thanks, and absolutely not, I was hoping more people would bet against me, so I could bet on myself for better returns.
23 traders in just a few days isn't bad at all, and I'm hoping interest picks up as it gets closer to the closing date. Thanks for creating it!
Update:
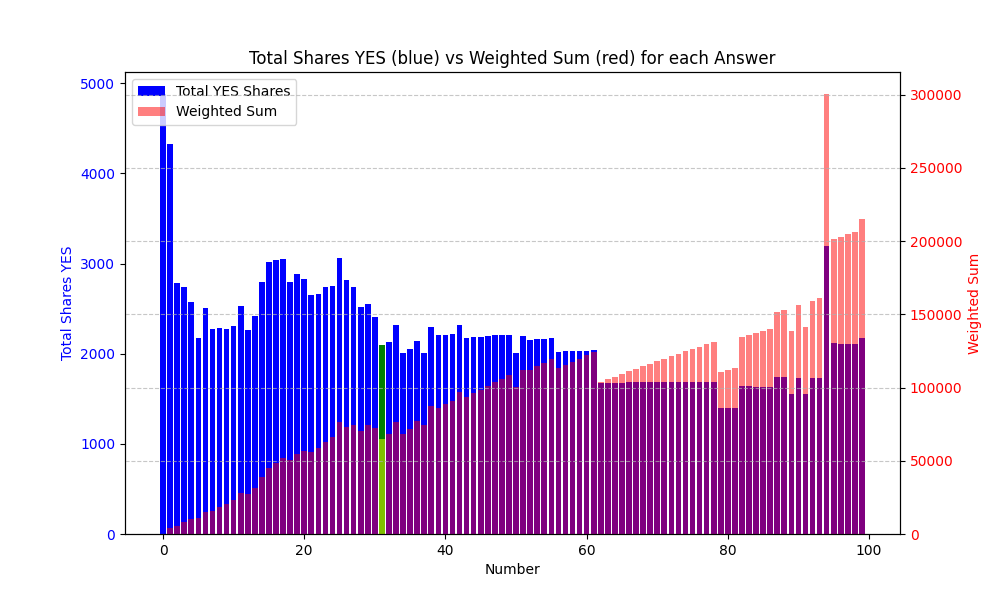
There's roughly 8,000 YES shares held of #0 and #1.
It only cost me 20 mana to purchase over 8,000 YES shares for the #s 77-86.
#0 and #1 are both currently at 7%, so let's test the Efficient Market Hypothesis.
@SavioMak that market resolved in November. I was inspired to put a new one up by the "public intellectual under/over rated" post that is a bit viral right now since it is basically another bounded rationality market (what do you think the market thinks). I didn't see any active similar markets.
@SavioMak I think the way this market is structured will change it's behavior for two reasons:
This market resolves based off the average number of YES shares held, whereas that market was based on the average of percentages. That makes this market much cheaper to affect, because purchasing relatively unpopular numbers will return an increasing number of shares relative to more popular numbers.
Since it's ONLY based on YES shares held, purchasing NO shares doesn't affect the outcome directly, but also makes it cheaper for people to buy more YES shares, increasing the potential effects of that number on the outcome.
While they are somewhat similar, I think the structure of this market creates two different incentives structures that might complement each other to create a more interesting resolution.
Whales will want to bet NO on impossible(66-99) or very unlikely numbers (0-5, 50-66), to earn guaranteed profits.
People betting on YES will want to accumulate more shares, as they become cheaper to purchase from the no votes.
In the other market, NO votes work against YES buyers, but in this one they work together.
@CalebW How does that change if someone spends 100 mana to buy 20,000 shares for the numbers between 89-98?
@CalebW Yeah, if you click the "# Positions" tab, next to "# Comments", it'll show Payouts for each number, which I believe represents the number of shares held.
@CalebW I don't think there is one, because it's calculated based on average shares held, and the way Manifold allocates shares to a purchase is based on its current probability, so there's an opportunity to make huge swings to the market as it gets close to its close by betting on the lowest probabilities to gain large amounts of shares.
For example, you bought 2,263 shares of 0 for 900 mana. I'd bought 819 for only 12 mana. So, I could gain more by selling those and buying other numbers, like I did to get 1,252 shares on 2 for only 10 mana.
Don't disagree with you that it's gonna be interesting! My reason for thinking the Nash equilibrium is in fact 0 is that at any time the 2/3rds average is above 0, there's a profit to be turned by buying some number lower than that average, which will itself pull the average down. Massive 0 accumulation is stable, everything else isn't. In practice, given finite balances, a whale could try to big brain a profit, but the easiest, lowest-risk way to do that would be a massive shock and awe zero buy up, rather than some clever construction of holding 0-value higher integers and fragile-y-profitable at best lower integers
@CalebW I guess massive 1 accumulation is also viable. Splitting my investment between 0 and 1 tyfs 🫡
@CalebW I think the flaw in that logic is that every additional dollar you spend on 0 gets you less of a share in return, so you reach a point where new entrants to the market, or even existing ones, have the potential for significantly greater gains by moving to a number other than #0.
People holding #0 won't be able to stop that, because when the percentage gets high enough, every dollar spent on a different number might return 10x in shares, skewing the average towards that higher number, and creating a greater incentive to leave #0.
I've spent about 250 mana to purchase roughly 25,000 shares, almost evenly distributed between #1 and #25. There are only ~2,300 shares on 0 and ~ 2,700 shares on 1, meaning 2/3rds the current average is somewhere around #7.
Because the total probability of the market is 100%, one number getting popular pushes others down to very small probabilities, making it advantageous to switch. Currently, I could buy ~1,800 shares of #98 for only 10 mana, meaning it won't take a whale to swing the market.
Simply put, the more you bet on 0 and 1, the more I can profit by tossing pennies on a range other numbers.