Will a quantum computer factor a 6-bit number by 2026?

1kṀ3407

Dec 31

88%

chance

ALL

Background: A 2019 paper showed the IBM Q System One was able to factor 15 and 21, but unable to factor 35 due to accumulating errors. Will a quantum computer factor a number greater than 31 by 2026?

Must use a non-classical algorithm like Quantum Fourier Transform/Shor's Algorithm to count, and without pre-compilation.

Update 2026-01-10 (PST) (AI summary of creator comment): The market will resolve based on whether a quantum computer factors a number greater than 31 by the end of 2026 (not before 2026 begins).

Market context

Quantum Computing

Get

1,000

to start trading!

People are also trading

Will a quantum computer break any widely used cryptosystem before 2030?

31% chance

Will a quantum computer factor the RSA-2048 challenge number before 2035?

45% chance

Will a quantum computer factor the RSA-2048 challenge number before 2030?

7% chance

Will a quantum computer factor the RSA-2048 challenge number before 2075?

78% chance

Will a quantum computer factor the RSA-2048 challenge number before 2040?

64% chance

Will a quantum computer factor the RSA-2048 challenge number before 2050?

78% chance

Will a quantum computer factor the RSA-2048 challenge number before 2100?

88% chance

Will a quantum computer factor the RSA-2048 challenge number before 2045?

66% chance

Will there be a quantum computer with 100,000 functioning qbits before 2035?

77% chance

In what year will a quantum computer factor the RSA-2048 challenge number?

Sort by:

Before 2026 or before the end of 2026? Title says one, close date says the other, description is ambiguous.

@Fion I think I meant by 2026 since that's what I said in the description and it's the resolution date I originally set. I've changed the title accordingly. Fortunately it doesn't look like anyone bet based on this resolving now.

@xyz what does 'without precompilation' mean here?

Does this count:
https://github.com/Curtisflo/QuantumFactorization

@QuantumObserver Also does it need to find all factors or just a factor?

@QuantumObserver I don't know enough about quantum computation to be honest, so I'm willing to take suggestions. The Github you linked says it uses it uses "classical post-processing" which I guess should be fine?

@xyz So here are screenshots of my runs of the code linked above for 77. It did use time on an IBM QPU (127 qubits) and produced correct factors. 1st screenshot uses an advantageous initial guess for the period finding (period = 2), but 2nd and 3rd show period = 3 and period = 10. Not as amazing, but still, able to find factors.

There are some philosophical issues here that Craig Gidney pointed out recently, once of which is that these numbers are so small that even an RNG output for the quantum parts of the algorithm could get you to the right answer. I don't see a good way to get around this without just voiding the question entirely.

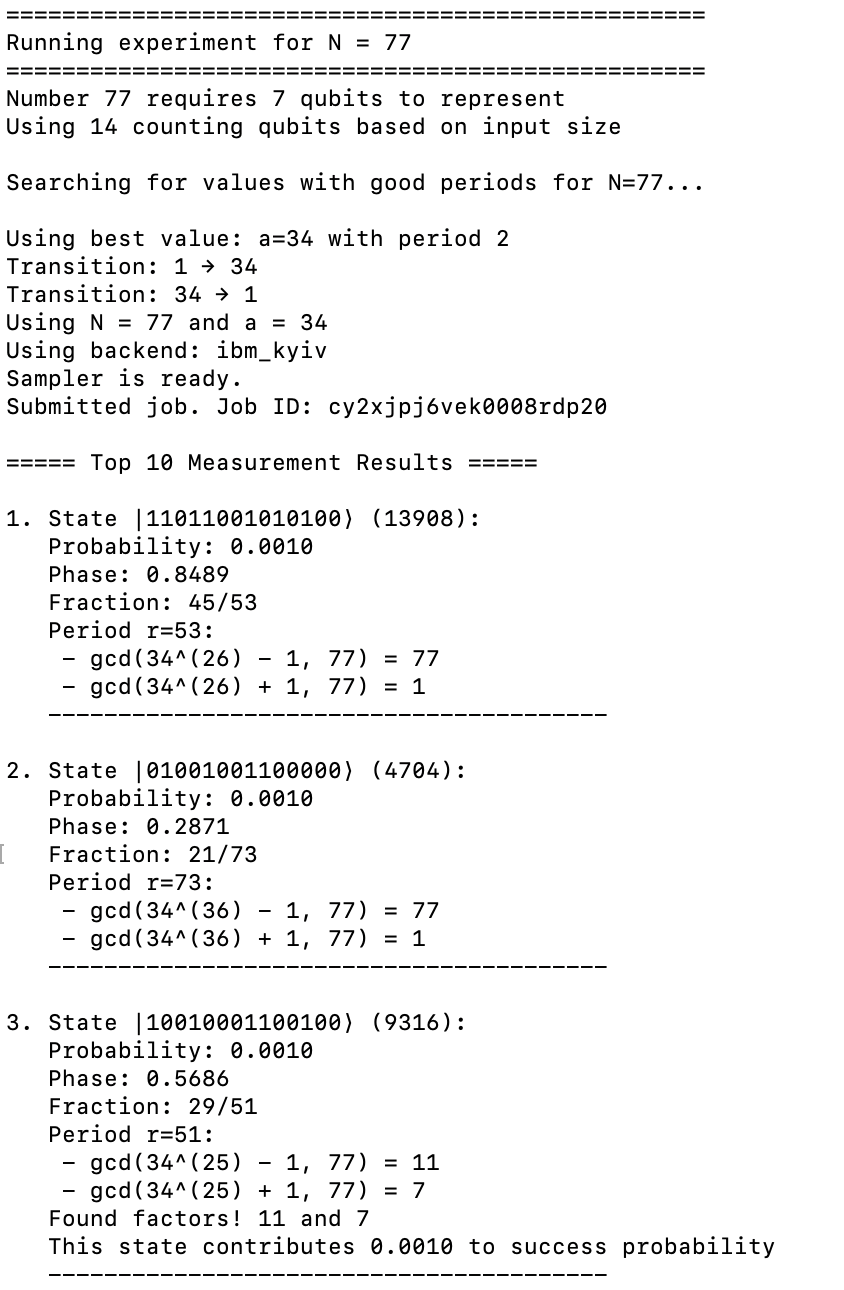
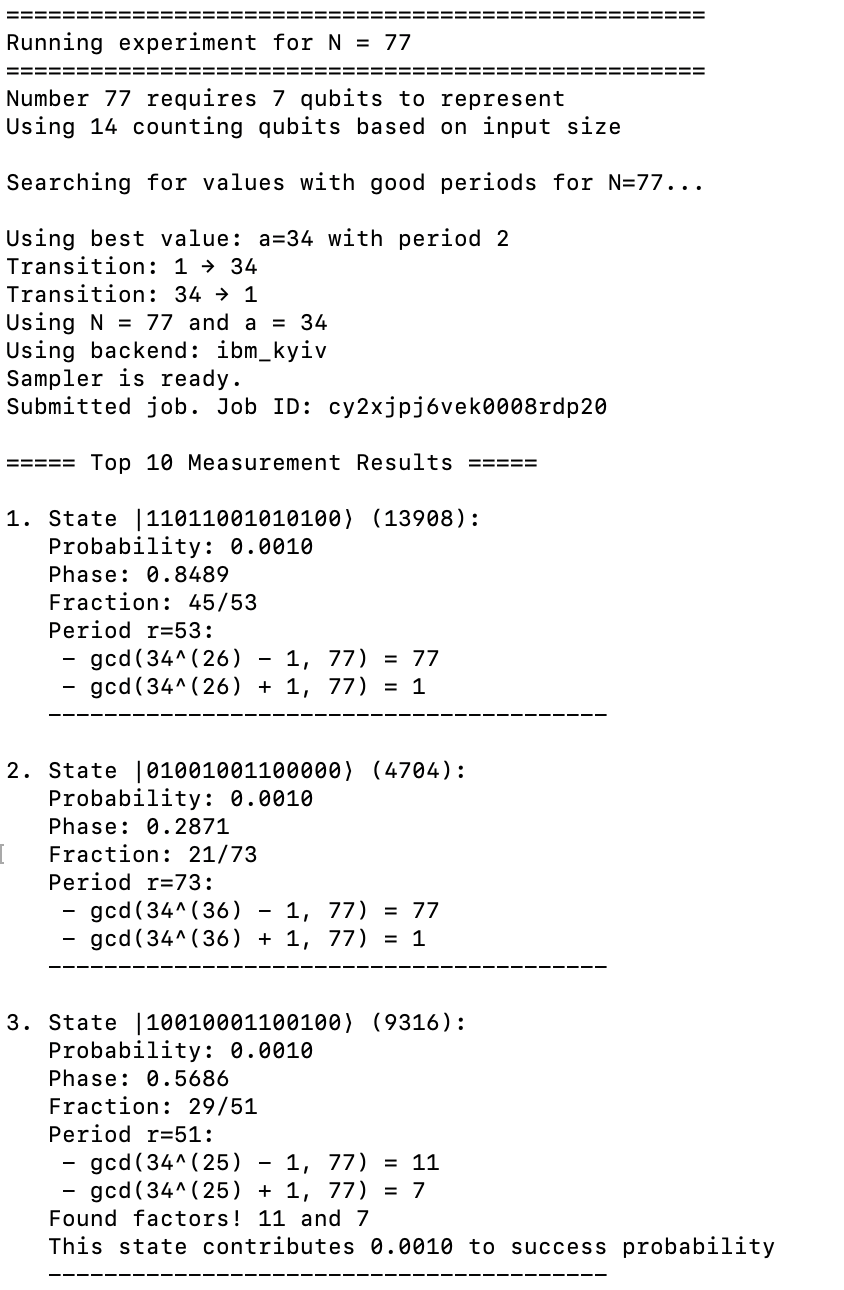
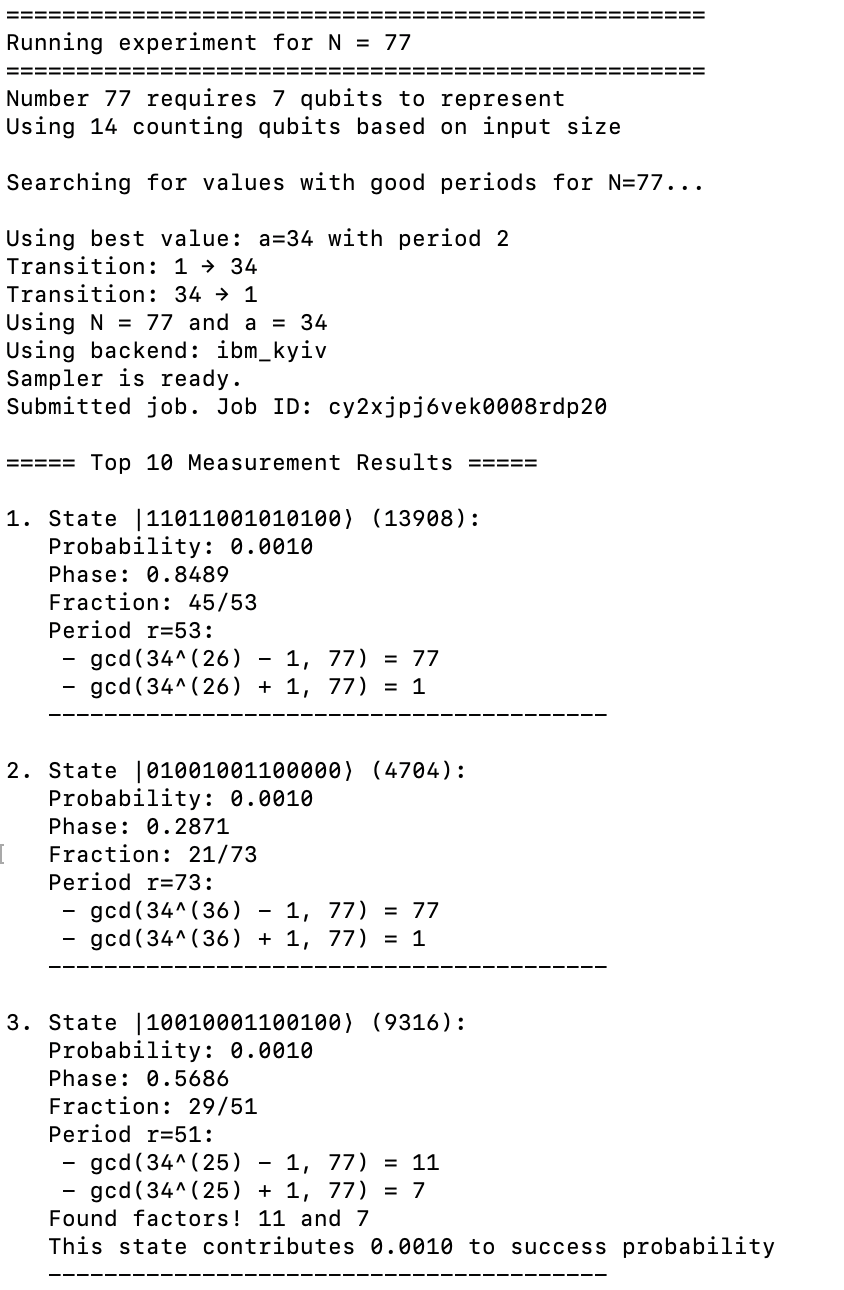
Turns out that larger semiprimes have been factored with adiabetic quantum computation and quantum annealing, so I’ve changed the question to refer exclusively to Shor’s, which was the original intention.