
Resolves to the PROB I assign to the notion of "IQ tests measure intelligence", which I will likely translate into "IQ tests measure g and g is intelligence" unless I get convinced that g is not a good way of thinking about IQ tests.
At the time of making this market, I feel like IQ tests measure general cognitive abilities (g), that is, things which are useful across a wide variety of cognitive tasks. So if there's something about your mind that is useful for both playing video games, understanding the meaning of words, being good at programming, etc., then that thing is going to be measured by IQ tests. However, I think it is limited what useful things IQ tests measure beyond g.
At the time of making this market, I think g is a big component in the everyday concept known as "intelligence", but I doubt that it is the only thing that people think of as intelligence. Other things I think people might think of as intelligence include:
Ability to deal with the most common situations everyone encounters, e.g. being socially skilled, not clumsy, having common sense (this is affected by g, but not identical to g, because factors that only affect ability to deal with common situations and don't generalize well would still be considered intelligence)
Ability to deal with the most common situations one uniquely encounters, e.g. being good at one's job, specialty and hobbies (this is again affected by g, but not identical to g, because factors that only affect this and don't affect general abilities would count as intelligence but not g)
Having stereotypically intellectual interests e.g. math, science, history, or high-brow politics (again this may be affected by g if g affects ability in those areas and ability affects interests, but it is not identical to g if there are unique factors that influence interests)
Agreeing with and defending society's taboos, even when they are wrong
This is not meant to be an exhaustive list, though I think these are the most convincing possible alternatives to g. Since it is not exhaustive, shooting down these possibilities might not entirely convince me that IQ tests measure intelligence, though since it is the most convincing alternatives, it would definitely update me upwards.
An example of something that would convince me that IQ tests measure the commonsense concept of intelligence would be a study showing that if you have ask informants who know people well to rank people's intelligence, then the g factor has a correlation of >0.8 with the latent informant consensus factor. It is currently my understanding that the correlation is more like 0.5-0.7, though I haven't seen a satisfactory study yet to be sure.
I will not be trading in this market.
🏅 Top traders
| # | Name | Total profit |
|---|---|---|
| 1 | Ṁ75 | |
| 2 | Ṁ39 | |
| 3 | Ṁ33 | |
| 4 | Ṁ18 | |
| 5 | Ṁ15 |
People are also trading
We can define categories however we want, but I think it’s useful to have a separate word for “ability to solve novel problems”. We need different words for the other things you listed:
cached thoughts about social context
Cached thoughts about job
Stereotypical preferences
Conformity preference
This really should have resolved 11 days ago, yet I haven't gotten around to resolving it yet, which is a bit of a problem. So I'm going to propose a resolution now.
When I originally created this market, I thought of it as having a low-ish probability - maybe 15%. The evidence I had seen at the time suggested that IQ measured something fairly central to intelligence, but also that g is not the whole story for intelligence. But I wasn't sure, and so I wanted to use this market to elicit better information.
Unfortunately, I didn't elicit much, so my probability stayed at around 15%. Part of the point was to come up with a more definite resolution by eliciting information, but that didn't really happen, so to better come up with a resolution, I've been researching this on and off for a while after the close.
As mentioned in the comments below, I had had a cached thought that IQ and informally assessed intelligence had a correlation of around 0.5 or so. Upon closer investigation, it's somewhat more complicated than that. IQ and informally assessed intelligence seems to have a correlation of maybe 0.2; the 0.5ish number instead seems to come from IQ and informally assessed intellectual orientation. For instance, this study finds an 0.4ish correlation between IQ and the personality trait "Intellect", which is particularly characterized by using fancy words.
So from this angle on things, the evidence for IQ correlating well with commonsense notions of intelligence is much weaker than I had cached, due to not inspecting the details and being properly critical about them. If we based things on that alone, I should probably un-update away from IQ and resolve this market to a low number.
HOWEVER, for unrelated reasons (I wanted to examine whether IQ tests are biased against black people in their choice of task focus), I also ended up doing a different survey to better investigate how people think of intelligence, where I asked people to name some examples of things they had done which require intelligence, encouraging people to pick the broadest difference of intelligence they believed in. The results from this survey were in line with my prior maximum likelihood, but they narrowed down my uncertainty in a way that partly updated in favor of IQ.
If this was an ordinary market, I would probably resolve this to NA due to weird contradictory evidence and unclear resolution. But since I explicitly stated in the criteria that I would assign it to the probability that I personally assign (with the implied understanding being that it's just my opinion and not guaranteed to be correct), I'm instead going to resolve it to PROB. And I think the PROB I pick is 25%.
I'll wait at least 24h before resolving so people have a chance to comment.
when I saw this market, having read some of your stuff in the past, I figured it'd depend a lot more on a very technical or idiosyncratic way of considering intelligence you had - if you just believed 'IQ = intelligence' like most people around here, you wouldn't create it. (not that you're wrong exactly!) so I didn't invest
@jacksonpolack I'm actually confused about why so many people bet yes, because I feel like I gave an explanation of why I was skeptical of YES in the market description. I assume it's because people didn't read it all/because it was too technical, but idk.
So, to an extent this market is a bit of a failure, because I had hoped it would stimulate some discourse about what we mean by intelligence or how measurement works, but not much has happened beyond the comments I have written. Still, I should obviously resolve the market, and hopefully my idea about how to resolve it will stimulate some discussion.
When I created the market, I proposed the following method for resolving it:
An example of something that would convince me that IQ tests measure the commonsense concept of intelligence would be a study showing that if you have ask informants who know people well to rank people's intelligence, then the g factor has a correlation of >0.8 with the latent informant consensus factor. It is currently my understanding that the correlation is more like 0.5-0.7, though I haven't seen a satisfactory study yet to be sure.
This still seems like a reasonable approach to me, at least as a first pass (see the various discussions in the comments in the market to learn more about specific details of my thoughts on it), though I am open to alternatives (as I hinted at in the market description and later explicitly said in the comments, I am open to arguments that this is the wrong way to think about the question, though this sort of forms a Schelling point for how to resolve the market if in doubt).
One study that was semi-privately sent to me after creating this prediction market is Mothers' Accuracy in Predicting Their Children's IQs: Its Relationship to Antecedent Variables, Mothers' Academic Achievement Demands, and Children's Achievement. It is not a perfect study, but I think it is worth going in-depth into this study so I can teach some ways of analyzing the issue.
The study itself is available on sci-hub, but the most important part of the study is this correlation matrix (showing how the variables that were measured in the study are related to each other):
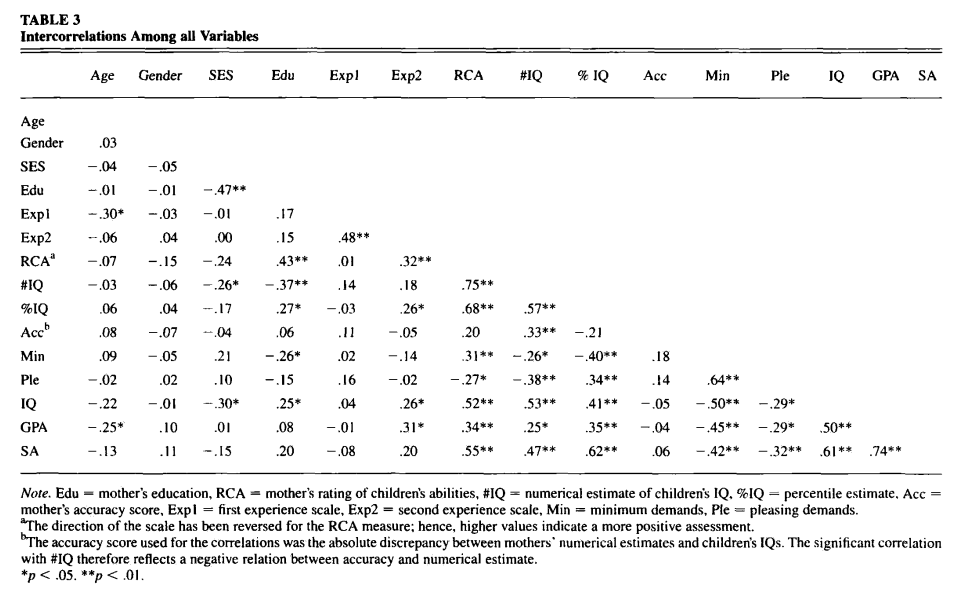
In particular, the #IQ column is centrally important, as it represents mother's estimates for their children's IQs, and the IQ row is also centrally important, as it represents the IQ scores of the children on the WISC-R IQ test. We might think of the mother's IQ estimates as representing the mother's notion of how intelligent their children are, in which case we see a correlation of 0.53 between mother's estimates and children's IQ, indicating that IQ is a nontrivial factor in intelligence, but that it is not the dominant factor, and therefore implying that the market should resolve NO (since it is less than the 0.8 that I proposed as a threshold).
However, that conclusion would be premature, because of measurement error. It seems easy to imagine that certain parts of the measurement went wrong. For instance a single question about the children's numeric IQ scores might be hard to answer for people who don't properly understand how normal distributions work, or it might be that some mothers have idiosyncratic definitions of intelligence, or so on.
Such a case would suppress the correlation between IQ and estimated intelligence. If r_{g, IQ} is the correlation between IQ tests and the "true trait" that IQ tests measure, r_{g, int} is the correlation between the true "true IQ" and the consensus notion of intelligence (i.e. the quantity we are interested in for this market), and r_{int, est} is the correlation between "true intelligence" and mother's estimates of intelligence, and r_{IQ, est} is the correlation between IQ and mother's estimates, then we'd often have something like r_{IQ, est} = r_{g, IQ} * r_{g, int} * r_{int, est}. The meaning of these variables may be kind of confusing, so see the diagram below.
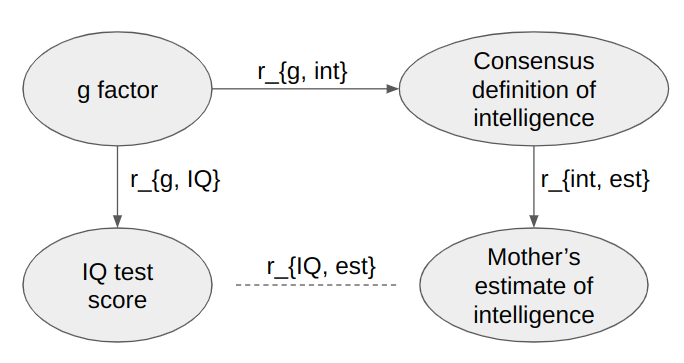
(Generally when you see causal networks like this, you can estimate the expected correlation between two nodes by multiplying up the effects along the paths between the nodes, and then adding the paths together. If you want to look up the technical details, the term to get into is "path analysis" or "structural equation modelling".)
If hypothetically we say that r_{g, IQ} = r_{int, est} = 0.73, then we can solve to get r_{g, int} = r_{IQ, est} / (r_{g, IQ} * r_{int, est}) = 0.53 / (0.73 * 0.73) = 0.99. By the criteria mentioned previously, that would get the market resolved to YES, except the 0.73 number was totally made up, so it's not to be taken too seriously.
But it gives us an important lesson: in order to fairly evaluate the question, we need to put some thought into measurement error. And perhaps counterintuitively, for a given observed correlation (e.g. the 0.53 number above), the less accurate the measurements are, the stronger the error-adjusted correlation is. This is essentially because measurement error makes it harder to see effects, so if you can see an effect despite strong measurement error, the effect itself must be really strong.
Estimating measurement error is kind of a headscratcher. If you don't know the true value for a measurement, then how can you know how accurate it is? The usual approach in psychometrics is to make multiple measurements that are hopefully independent conditional on the true value getting measured, and then assuming these measurements correlate due to the true accuracy of the test, while the unique variance is the measurement error. This approach can be somewhat criticized, and again I'm open to debate about it, but it's the one I wrote in the original market criteria, so it's the one I will go with as a Schelling point for this issue.
Let's start with measuring the accuracy of the IQ test. There are various studies that provide ways of learning about it more straightforwardly, but let's instead fit a one of the simplest models for measurement error, the latent factor model, as a learning exercise.
In the study, in addition to IQ, there were two other tests of cognitive abilities: grade point average (GPA) and the Stanford achievement test (SA). Unlike IQ, GPA and SA are meant to measure what you've learned in school, so they are not technically the same thing. However, in practice they are correlated and people often use one as a proxy for the others, so just hypothetically to play around, let's pretend that they are all measures of the same thing, and see what we can learn.
The latent factor model assumes that each variable (IQ, GPA, SA) has a "factor loading" (λ_IQ, λ_GPA, λ_SA) representing the degree to which they correlate with a shared latent variable (which I suppose we can call Ability or something...). The correlations between any two of the variables should then be the product of their loadings. So for instance the correlation between IQ and GPA should be λ_IQ * λ_GPA.
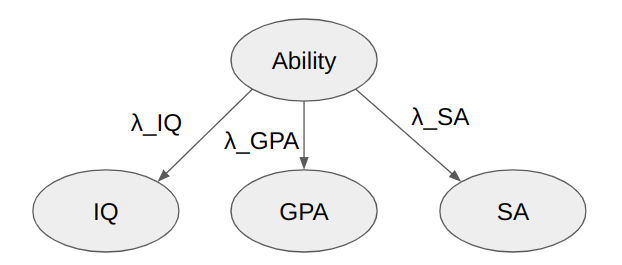
This gives us three equations (λ_IQ * λ_GPA = 0.5, λ_IQ * λ_SA = 0.61, λ_GPA * λ_SA = 0.74) for three unknown variables, which we can solve to obtain e.g. λ_IQ = sqrt(r_{IQ, GPA} * r_{IQ, SA}/r_{GPA, SA}) = sqrt(0.5*0.61/0.74) = 0.64. And similarly λ_GPA = 0.78, λ_SA = 0.95.
So one accuracy estimate we can use for the IQ test is 0.64. We'll evaluate later whether this is a good accuracy estimate, but for now let's consider how to estimate the accuracy of the mother's evaluations of their children's IQs.
The obvious choice would be to use the latent factor model again, but we run into the difficulty that there are only two intelligence estimate variables (#IQ and percent IQ), which leaves us with 1 equation and 2 unknowns, making the system underdetermined. One neat approximation one can do in this sort of case is to assume that the two variables are equally accurate (two loadings/λs are the same), in which case one can estimate λ = sqrt(r) where r is the correlation. This would give us λ = sqrt(0.57) = 0.75. Another approach is to pick some additional third variable to throw in, e.g. we could pick actual IQ. This gives us λ_#IQ = sqrt(0.57*0.53/0.41) = 0.85, and λ_%IQ = sqrt(0.57*0.41/0.53) = 0.66.
So, if we estimate the accuracy of the IQ test as λ_IQ = 0.64, and we estimate the accuracy of the mother's estimates as 0.85, then what happens to the correlation of 0.53 as we adjust it for measurement error? We get 0.53 / (0.64 * 0.85) = 0.97, which is clearly above the threshold of 0.8. So does this mean the market should resolve YES?
Nope, because this was just an exercise in how I go through the numbers. It turns out that these numbers can't literally be correct. For instance if the SA test has an accuracy of 0.95 of measuring the same thing that IQ tests measure at an accuracy of 0.64, then it seems like we should expect mother's evaluations of children's intelligence to correlate 46% more with the SA test than with the IQ test. Yet instead they seem to correlate about equally closely. What went wrong?
What went wrong is that we just grabbed the most convenient available notion of measurement error, without thinking through whether it was the appropriate one for the task. Some notions of measurement error may be context-specific, or may be limited to being upper bounds or lower bounds, and if we don't take this into account, we may bias the calculations. So let's be a bit more careful in the analysis:
(...to be continued in a subcomment because I am running out of comment space...)
(...)
When we fit an ability model to (IQ, GPA, SA), we have to consider the causal relations. The real relationship is probably something like this:

The interpretation of λ_GPA and λ_SA are the same as before, but λ_IQ has split into two variables, L_IQ representing the accuracy with which the IQ test measures general cognitive abilities, and e_g which represents the degree to which general cognitive abilities contribute to scholastic knowledge. In particular, this means that our previous estimate for the accuracy of the IQ test is an underestimate. And remember, the lower the accuracy of a test, the higher the accuracy-adjusted correlations are, so if the accuracy estimate is biased downwards, that means the accuracy-adjusted correlations are biased upwards.
When I said to adjust for the accuracy of the IQ test, I specified that it should be with respect to the g factor, i.e. the L_IQ part of this chain. The L_IQ part of the accuracy can be quantified using the "omega hierarchical" notion I brought up elsewhere in the comments. According to this study, the omega hierarchical for WISC-R is something like 0.81-0.85, which suggests we take a L_IQ = sqrt(0.83) = 0.91 as our estimate for the accuracy of the IQ test.
As a first pass, this very much reins in our estimate of the accuracy of IQ tests as a measure of intelligence. Before, we estimated them to have an accuracy of 0.53 / (0.64 * 0.85) = 0.97, but now we would estimate them as having an accuracy of 0.53 / (0.91 * 0.85) = 0.69, which is within the 0.5-0.7 range that I originally described as my expectation for the market. Since this is less than the 0.8 I described as a threshold, this suggests that the market should resolve NO.
EXCEPT... yes, we've seen how the naive approach underestimated the accuracy of the IQ tests, but surely the naive approach was also wrong about the accuracy of the mothers? Yep! In particular, the naive approach overestimates the accuracy of the mothers, which biases the adjusted correlation downwards.
To estimate the accuracy of the mother's evaluations of their children's intelligence, we looked at the correlation between their ratings of their children's intelligence in an absolute quantitative manner, versus in a percentile manner. This may very well adjust for certain kinds of error, such as lack of familiarity with the ways they were asked about the children's intelligence. However, it does not adjust for other kinds of error which are consistent for the mothers, such as idiosyncratic definitions of intelligence, or biases towards their own children, or similar.
A primary way personality psychologists know for identifying this type of measurement error is to ask multiple raters, and this is also the method I suggested in the OP, so it forms the Schelling point for how to estimate the error. Unfortunately, this study only asked about the mothers' views, so we'll have to go beyond the study to estimate further. This is in fact the thing I was most uncertain about when I made the original post, so I would love additional input.
One line of evidence I have is this paper:

... which finds that people agree about how intelligent people are about as much as they agree about just about any other personality trait, with a few exceptions (emotional, talkative, quiet and dominant achieving higher agreement, I assume because they are particularly obvious). Unfortunately this does not measure estimated intelligence in the same way that the study of mother's estimates does, so the quantities are not directly transferable.
... I need to go prepare dinner now. But the basic summary of what I'd write next is that I am still uncertain about what exactly the relation is. Somewhere along the line I picked up the idea that IQ tests correlate at like 0.5 with perceived intelligence, and that different raters agree with each others about perceived intelligence at a rate which suggests that perceived intelligence has an accuracy of 0.77. If we use these numbers as our accuracy of perceived intelligence, then this gives us an IQ test accuracy of 0.5 / (0.91 * 0.77) = 0.71, which again is not enough for the market to resolve YES. However, I cannot immediately think of where I picked up this idea, and I don't want to resolve the market NO without a source, so the resolution will have to wait for a bit.
Gah, I keep typing up half a comment making a case for the market to be resolved in some way, then checking up on the details and getting dissatisfied with the available data. Kind of surprising how poorly studied this sort of question seems to be, considering how much drama there has been over the validity of IQ tests.
@Boojum Interesting article: https://www.vox.com/platform/amp/2016/5/24/11723182/iq-test-intelligence
"Ask yourself this question: would the average smart person perform better than the average dumb person on an IQ test. If you're answer is yes, resolve as YES"
@Boojum Variants of this argument are valid under some circumstances but not all circumstances. I think it is worthwhile to analyze what circumstances it is relevant to understand things well.
First, imagine if the people we'd classify as smart score an average IQ of 105, while the people we'd classify as dumb score an average IQ of 95. Does that make IQ a measure of intelligence? I would say no, because there is like 75% overlap between the groups. It has an error rate of 25%, which is better than the the rate of 50% that you'd get by chance, but still very high.
So it's not enough to have a difference in IQ based on intelligence. Rather they must in some sense be big. For instance, if everyone can be classified into "smart" or "dumb", and smart people consistently score higher in IQ than dumb people, with something like a 30+ point gap between their averages, then it starts looking reasonable.
And yes, I could easily believe that if you take people who are known for being smart, and people who are known for being dumb, then they would have basically non-overlapping IQ ranges. So that means I should resolve the question to "yes", right? Not so fast. This argument is likely valid if intelligence forms a binary smart/dumb distribution, but are you right about it doing that? I don't think so, with several pieces of evidence:
If intelligence is binary, then under ordinary circumstances things like g or IQ which are strongly correlated with intelligence would also tend towards being bimodal, or at least be distributed in a way that is not so peaked on the center. However IQ is normally-distributed. (There are some complications to this argument which we can go into downstream if you want, but I think it is basically true.)
Our primary theories about how variation in g works is that it comes from lots of small genetic variations in the things like brain size or brain function which have small effects on general performance. But many small variations would tend to produce continuous distributions, rather than the binary distributions you are suggesting.
I think we can usually come up with more gradations of observable intelligence than just smart/dumb, e.g. Richard Feynman was very smart, Average Joe is not so smart, and then some people are kind of dumb.
Suppose therefore for greater realism that intelligence is not binary, but instead e.g. normally distributed. What then goes wrong with your approach of comparing people who are smart to people who are dumb? Essentially, you will end up using different intelligence thresholds for smart vs dumb people, which will exaggerate the correlation between IQ and intelligence.
For instance, suppose people develop a reputation for being smart when they are 2 standard deviations above the mean of intelligence, and people develop a reputation for being dumb when they are 2 standard deviations below the mean in intelligence. In that case, if r^2 is the variance of intelligence that is due to g, then smart people would be expected to have a higher g-score of around 4 r^2, which means that if e.g. variation in intelligence is only 50% due to g, then smart people would still be 2 standard deviations higher in g than dumb people, making them pass (my modified version of) your test, yet still making this market resolve NO.
@tailcalled Clusters are fuzzy things.
Obviously, there are no strict 'smart' and 'dumb' clusters of people, just like there are no strict 'tall' and 'short' clusters of people. IQ tests are not claiming the former, just like rulers are not claiming the latter. Still, it makes perfect sense to describe rulers as good measures of tallness, and showing their ability to distinguish 'tall' and 'short' people to be an argument in their favor.
Tallness is very unimodal, yet how can anyone claim this means anything really relevant about test's accuracy of distinguishing where in this unimodal distribution someone resides?
A measuring tape is a good measure of length, (among other things) because it distinguishes well short and long things.
Speaking of the correlation between IQ and intelligence is somewhat akin to speaking of the correlation between height and the length your measuring tape measures when measuring your height--one is simply the test to measure the other. To claim that it does not is confused. Could you slip on a banana and measure a tall person as bellow average? Sure. Would that make the measuring tape not a measure of height? What? Even if you slipped half the time, it would still be a measure of height, it would simply be an additional fact that the you-measuring-tape combo is an imprecise measure of height. IQ is a somewhat imprecise measure of intelligence, like all measures of all things, but still! It does measure it!
(Upon sending everything and asking whether I missed something, GPT-4 is asking me to add that IQ tests are biased and do not measure well all aspects of intelligence like creativity and EQ. I agree to some extent.)
@BionicD0LPH1N I agree with a lot of what you are saying. Just to clarify, my comment was specifically responding to Boojum's argument that a group difference is sufficient to prove that they measure intelligence, not meant to cover intelligence measurement more generally. (I plan on writing a top-level comment on this market soon where I give my current views and invite for debate before resolving. However it will take a bit to write and I have a few other things to do, so it won't happen immediately.)
"Still, it makes perfect sense to describe rulers as good measures of tallness, and showing their ability to distinguish 'tall' and 'short' people to be an argument in their favor."
I think there are various claims to measuring tallness with varying levels of strength:
Rulers are a non-useless proxy if you want to find tall people (If the correlation r between the ruler measurement and a person's height is meaningfully r >> 0.)
A significant part of why some people are considered tall by ruler measurements is because they are actually tall (r^2 >> 0)
There is not really much other reason than height for why people get the ruler measurements that they get (r^2 ≈ 1)
Given a ruler measurement, you accurately know a person's height, as nothing but height really influences ruler measurements of height (sqrt(1-r^2) ≈ 0)
IIRC think the correlation between ruler measurements and actual height is something like r=0.97 (there's some interesting questions I won't get into yet about how this sort of number comes up), which makes them excel at properties 1-3 and perform OK on property 4. (And they also satisfy a bunch more properties, which are really fascinating to think about but not so relevant to the question).
However, Boojum's argument would only show that rulers satisfy the first criterion, not the other ones (since his argument is only a direct test of the first one). Of course you are right that Boojum's argument is evidence of the latter ones, but only because it rules out truly astrological measurements, not because this is a serious part of an incremental research program to show that it satisfies the stronger properties you'd expect of many measurements.
An additional complication comes in if you want to use a ruler to measure e.g. weight via height as a proxy. Let's say that weight is determined by height, adiposity and muscularity. You can use a ruler measurement to get you an accurate idea of a person's height, but their height will only be imperfectly correlated with their weight, so again we have similar thresholds of measurement quality to the above, but with different interpretations:
Height is a non-negligible contributor to weight (r >> 0.)
A significant part of why some people have the weight they have is because they are tall (r^2 >> 0)
There is not really much other reason than height for why people are the weights they are (r^2 ≈ 1)
Given a height measurement, you accurately know a person's weight, as nothing but height really influences weight (sqrt(1-r^2) ≈ 0)
Looking it up, the within-sex correlation between weight and height is something like 0.5. This implies that we definitely have property 1, and kind of have property 2. (Interesting TIL from this: it might be hard for a ruler to both satisfy property 4 wrt. height and satisfy property 2 wrt. weight, because they are both close to the same threshold.)
A thing I should add:
There's an interesting question of how strong properties a measurement method must have before it is considered a real measurement. I don't think it would be considered acceptable to be missing properties 1 and 2 (though I would be open to hearing arguments, e.g. if there are commonly accepted measurement which lack those properties then I might change my mind). I'm pretty sure IQ tests satisfy properties 1 and 2, so I expect IQ tests to be better measures of intelligence than rulers are of weight.
It gets more complicated with properties 3 and 4. I don't think anyone claims IQ tests satisfy property 4, and I don't think many people would require measurements to satisfy property 4 in general. It's a very strong property that we only get with some of our best measurement methods. So the controversy is mostly about property 3.
The requirements for property 3 might be a YMMV thing where people disagree a lot. If my opinion on property 3 is very controversial, then I might change my mind or run a poll or something to make the resolution more aligned with what people think. But my current thoughts are:
If a proposed measure totally fails property 3, then it can't really be considered a measure. For instance, height as assessed by a ruler is not a measurement of weight among ordinary people, because weight isn't really dominated by height.
On the other hand, we can be a bit generous, e.g. taking the ruler as an example, it seems the threshold for satisfying a property should be around an 0.25 distance from the target value. Which would suggest that IQ should have an r^2 of 0.75 for intelligence to count as a measure of intelligence. This strong of a correlation looks as follows:
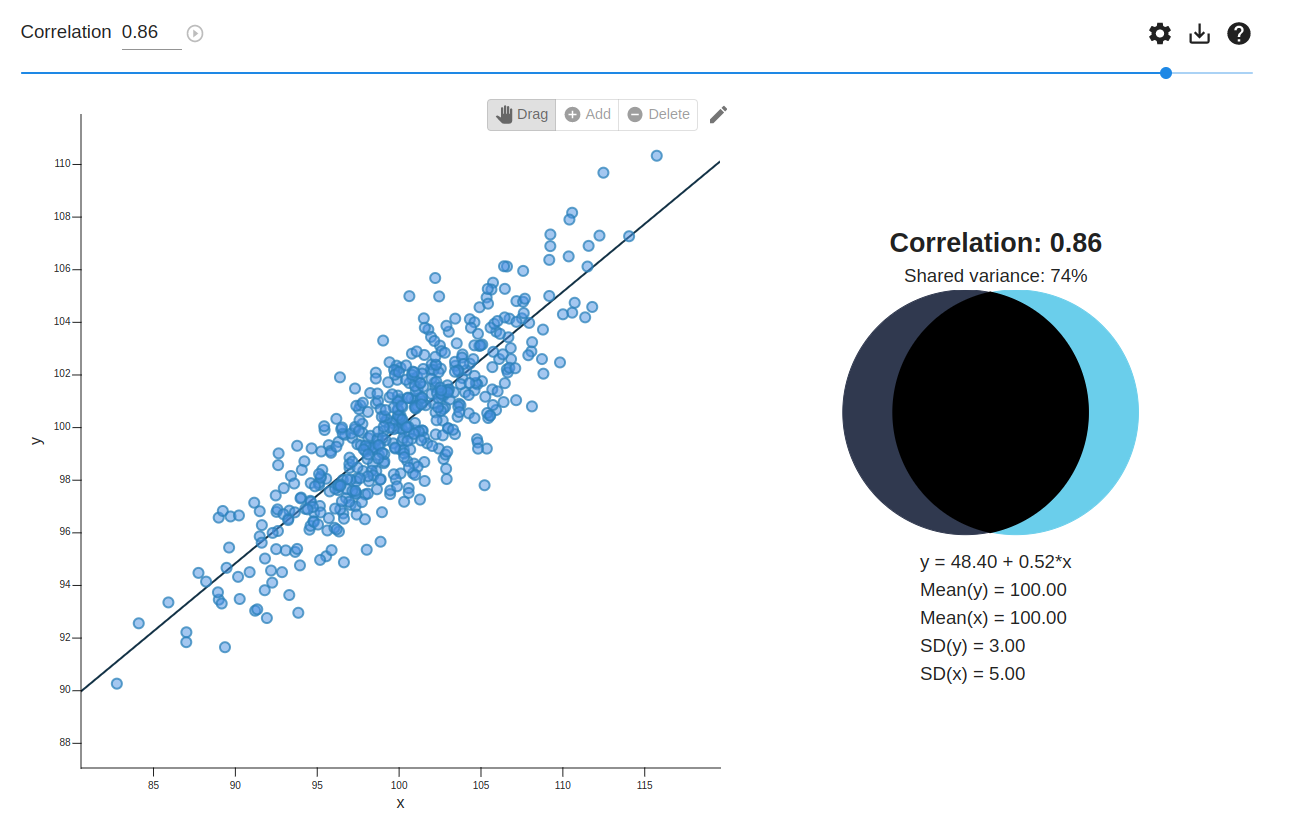
There are two ways we can be more generous than that. First, not all measurement errors are equal. If a measurement error is random/uncorrelated with everything else, then it is easier to take into account in a bunch of ways (e.g. you could reduce it by making additional measurements). And if a measurement error is clearly labelled when using the test, then it can be taken into account when applying it. (These two are closely related because one of the main ways one identifies measurement errors is by measuring in multiple ways and seeing how closely correlated those measurements are.) So we should to an extent be willing to adjust for that.
My OP suggests that we should take a latent correlation of 0.8 to be sufficient evidence for a YES resolution. This is weaker requirement than the diagram I shared above, both because "latent correlation" is fancy psychometrics lingo for "adjust for known measurement errors", and because 0.8^2 = 0.64, implying an error tolerance of 0.36 instead of 0.25.
"Speaking of the correlation between IQ and intelligence is somewhat akin to speaking of the correlation between height and the length your measuring tape measures when measuring your height--one is simply the test to measure the other."
We can still speak of the correlation between the test and the property, though?
The simplest variant of this would be if you have some very accurate test that you can use as a ground truth. For example, I once saw a study investigating the accuracy of self-reported weight, by having a bunch of people report their weight and then get weighted in the doctor's office for comparison.
If you don't have a perfect ground-truth test, then it is more difficult to estimate the correlation between the test and the thing getting tested, but that doesn't stop people from trying. The thing I see people most commonly cite is the test-retest reliability, i.e. if you get measured twice, how accurate highly correlated is that. This corresponds to the r^2, and for high-quality IQ tests it's something like 0.9.
Which in turn would suggest that the r is something like 0.95, except test-retest reliability is sort of an astrological notion of validity. (Literally! Your star sign presumably has a test-retest reliability of 1, but that doesn't make star sign a valid measure of anything.)
IQ tests commonly claim to measure the g factor, a characteristic which makes you better or worse at a wide variety of cognitive tasks. Psychometricians have come up with a notion called omega hierarchical for quantifying the validity of a measure of such a factor. Roughly speaking it works by using the correlations between performance on different tasks to measure the degree to which different tasks load onto the g factor, and then computing the accuracy of a given test battery from the loadings of the tests in the battery.
When I wrote the question, I had the impression that the omega hierarchical for a good IQ tests is something like 0.86, which corresponds to a correlation with g of sqrt(0.86) = 0.93. I'll probably double-check this before making a serious case for resolving the market, though.
@tailcalled Thanks for your answer. I agree with pretty much everything, and am embarrassed to say that I did not read the market’s description before sending the previous message. Oops.
@tailcalled Without checking, would you know and care about the difference between a psychometrist and a psychometrician, if there’s one?
@yaboi69 Prior to checking the distinction: A priori I don't necessarily care about either, because while formal psychometri* training educates people out of some common misconceptions, I have the impression that it also educates people into some strange approaches.
Of course you asked about the distinction between psychometrist and psychometrician, not about my opinion on psychometri*ses vs normies. I don't know what the distinction refers to. If I had to guess the second is someone who designs and administers psychological tests such as IQ tests and personality tests, because I feel like I've heard that word used in that context, whereas I don't think I've heard the word psychometrist. Maybe psychometrists work in psychophysics or something. I would have assumed they were synonymous if not for your question.
After checking the distinction: Ok, so psychometrists are the ones administering the tests, psychometricians are the ones designing and administering the tests. This might reveal my ivory tower tendencies since I've mostly read into the latter. I would probably be inclined to trust psychometrists relatively more on questions related to test administration (such as "are there sometimes kids in school who don't put in enough effort to do well on tests even though they could?") and psychometricians relatively more on questions related to psychometric theory (such as "are cognitive abilities multidimensional?").
@tailcalled Yeah, I’ve never heard about the distinction either, or long forgotten it. Don’t worry about it, it’s more of an inside joke that is really not worth more than 5 seconds. (Someone accused someone else of credential fraud in part because of this semantic issue.)
On a (just slightly) more serious note, do you have any thoughts on Taleb’s takes on IQ? (I’m not asking with a deep purpose either, just picking your brain, I’ll appreciate even a very short answer like “mostly agree/disagree”.)
@yaboi69 One of Taleb's most repeated criticisms is that the correlations involved with IQ are very low in terms of information content.
The core thing information is designed to measure is how long "messages" can be sent through a channel. So basically in this critique, Taleb is saying that if you had a message you wanted to send, encoded it into a number x between 70 and 130, took a smart person (e.g. IQ 130), gave them a precisely controlled amount of brain damage to set their IQ to x, and then transported the person to where you wanted to send the message to, and had them perform work, and decoded the message from the quality of their work, then the fact that IQ carries ~no information means that you can't really use this as a protocol for sending messages of any nontrivial length.
I agree with Taleb that precisely delivering brain damage and then decoding that brain damage using work performance is a terrible message-passing protocol and that you'd be better of using the internet or something. However, I have never seen a fan of IQ advocate for this message-passing protocol, and so I think his argument is absolutely ridiculous.
Another quite repeated criticism is that IQ isn't a measure of real-world performance but instead of "intellectual yet idiot" tendencies. I would agree that IQ isn't a measure of real-world performance but instead of the g factor. However, I don't see any reason to think that the g-factor leads to idiocy in the real world; instead it seems like the g-factor is useful across many contexts, including heavy-tailed contexts such as trading. Of course the g-factor isn't everything, it's just one important factor.
He also had a bunch of other criticisms than those, but I can't address all of them here.
This may also be of interest: Are smart people's personal experiences biased against general intelligence?
@tailcalled I think there's a decorrelation in the tails between intelligence-as-cleverness and intelligence as the ability to generate deep insights. I remember seeing some quotes at some point on both Grothendieck and Einstein roughly saying they saw themselves as less capable of generating immediately clever insights than their peers (peers here being a very high bar i.e. ~famous mathematicians). But, seems to me, this decorrelation occurs well before the Grothendieck level of ability c.f. for instance, the distinction between mathematicians inclined to theory building vs problem solving.
Now re:IQ, I'd expect such tests to track cleverness, and almost entirely miss ability to generate deep insights when these two come apart. Would be interested to know if there's empirical evidence on this point. Though I assume quantifying ability to generate insight is well beyond current methods, so data would have to be observational!
@JacobPfau I think interest and motivation is a large confound here, where people do have strong preferences and so optimize their abilities along different axes. It's not clear to me how much of this effect interest/motivation explain away.
@JacobPfau I think it's tricky to say much about this from a psychometric perspective because generating deep insights doesn't lend itself well to measurement. (Psychometrics tends to be very data-driven, by the way.) So what I have to say is going to be speculative.
One thing to remember is that IQ tests measure general abilities. This matters a lot for the case of e.g. generating insights into physics, because I bet Einstein and all other physicists have a bunch of specific characteristics that make them way better at physics than their IQ would suggest on its own (both better at being clever and better at generating deep insights). For instance they have done a lot of physics problems and had a lot of physics education.
I expect that these specific characteristics make them both better at quick, clever, superficial solutions to physics questions, and at long, wise, deep insights in physics. Though there is some decorrelation (e.g. maybe wide experience leads to more deep insight).
But here we talk about cleverness and deep insights in the abstract, rather than specifically to physics. This requires some way to abstract away the specific topic of physics. For instance one could use the same approach that IQ tests use, of considering a general factor that permits deep insights across many topics. But I think that's hard to even investigate the existence of, because deep insights are too rare and difficult to measure.
of course, it's hard to be interested (in a non-popsci way) in particle physics when you can't understand it. and even if you maintain that interest, you're more likely to become a trisector than einstein.
and interest might be part of what contributes to 'g' anyway, someone who's inextinguishably interested in 'figuring things out' might, naturally, in whatever environment, accumulate more of the 'knowledge' required to be intelligent in any specific topic.
As per the market title, this should resolve to YES, and as per the market description, this should resolve to NO. There undoubtedly are aspects of what people think of as intelligence that are not or poorly measured by IQ tests. Mosr of them probably correlate with IQ, but I would really doubt they’d correlate at 0.8, that’s very high.
@BionicD0LPH1N Note that it is common in psychometrics to get correlations in the 0.7-0.99 range. Test-retest correlations for full-scale IQ is something like 0.9, some studies claim that the g-factors of different IQ test batteries correlate at like 0.99 (though I've been meaning to look into whether they are making a specific methodological error and consider it plausible that they actually "only" correlate at 0.9ish), etc.. This study found that the g factor had a correlation of 0.79 with the general factor underlying video game performance: https://www.sciencedirect.com/science/article/abs/pii/S0160289618301521
I should also note that it's not that all of the aspects of intelligence have to correlate well with IQ in order for the market to resolve positively. It is sufficient if overall intelligence correlates well with IQ. Like you could imagine that intelligence is made out of 5 independent factors, each of which correlates at 0.45 with IQ. If that is the case, then the market would still resolve yes, because that would mean that overall intelligence has a correlation of 1 with IQ, even though each of the 5 independent factors only has a correlation of 0.45.