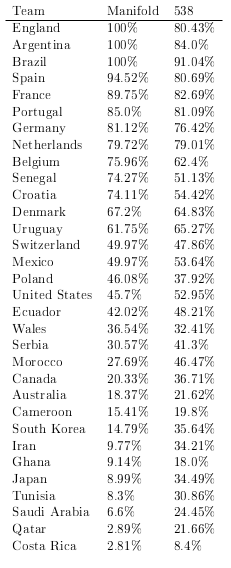
This market resolves YES if the Brier score for the predictions of the manifold market below is lower (lower is better) than that for the FiveThirtyEight 2022 World Cup Predictions: https://projects.fivethirtyeight.com/2022-world-cup-predictions/
I will compare the predictions before the start of the World Cup (November 20).
By the nature of the manifold market (multiple choice with 16 answers resolved with equal percentage) I will multiply all probabilities in the market by 16. I will assume that any probability larger than 6.25% percent in the manifold market is equal to 1.
Since I will be calculating the scores, I won't bet on the market after I gather the data (November 20). The market resolves at the end of the group stage when all teams for the Round of 16 are determined.
Brier score: https://en.wikipedia.org/wiki/Brier_score
Manifold market to compare:
🏅 Top traders
| # | Trader | Total profit |
|---|---|---|
| 1 | Ṁ21 | |
| 2 | Ṁ8 | |
| 3 | Ṁ6 | |
| 4 | Ṁ5 | |
| 5 | Ṁ4 |
People are also trading
if you want to check:
outcomes = {"Qatar":0,
"Ecuador":0,
"Senegal":1,
"Netherlands":1,
"England":1,
"Iran":0,
"United States":1,
"Wales":0,
"Argentina":1,
"Saudi Arabia":0,
"Mexico":0,
"Poland":1,
"France":1,
"Australia":1,
"Denmark":0,
"Tunisia":0,
"Spain":1,
"Costa Rica":0,
"Germany":0,
"Japan":1,
"Belgium":0,
"Canada":0,
"Morocco":1,
"Croatia":1,
"Brazil":1,
"Serbia":0,
"Switzerland":1,
"Cameroon":0,
"Portugal":1,
"Ghana":0,
"Uruguay":0,
"South Korea":1}
print("Brier fivethirtyeight:", sum([(fivethirtyeight[country] - outcome)**2 for country, outcome in outcomes.items()])/32)
print("Brier manifold market:", sum([(mm_[country] - outcome)**2 for country, outcome in outcomes.items()])/32)
Just downloaded the data. These are the probabilities that I will be using:
mm = {'England': 1,
'Argentina': 1,
'Brazil': 1,
'Spain': 0.9451968360534888,
'France': 0.8974907339737943,
'Portugal': 0.849977244235089,
'Germany': 0.8112415168267147,
'Netherlands': 0.7971968295073112,
'Belgium': 0.7595755431348061,
'Senegal': 0.7426855519809036,
'Croatia': 0.741065876527692,
'Denmark': 0.6719708710471769,
'Uruguay': 0.617516701467408,
'Switzerland': 0.49974494455889923,
'Mexico': 0.49965919586782787,
'Poland': 0.4608358796614559,
'United States': 0.45698850032681404,
'Ecuador': 0.4202289531028565,
'Wales': 0.36538907075213484,
'Serbia': 0.3057351303302865,
'Morocco': 0.27690844073942406,
'Canada': 0.20328431337571382,
'Australia': 0.18374603476500043,
'Cameroon': 0.15410561203952933,
'South Korea': 0.14789233306591248,
'Iran': 0.09774239358780965,
'Ghana': 0.09141480094632379,
'Japan': 0.08992401674617002,
'Tunisia': 0.08298078235641886,
'Saudi Arabia': 0.06596123866028777,
'Qatar': 0.028929836130672053,
'Costa Rica': 0.02812887522247895}
fivethirtyeight = {'Brazil': 0.91045,
'Spain': 0.80686,
'France': 0.82686,
'Argentina': 0.83995,
'Portugal': 0.81087,
'Germany': 0.76424,
'England': 0.80426,
'Netherlands': 0.79006,
'Denmark': 0.64835,
'Uruguay': 0.65274,
'Belgium': 0.624,
'Croatia': 0.54419,
'Switzerland': 0.47861,
'United States': 0.52953,
'Mexico': 0.53636,
'Senegal': 0.51129,
'Ecuador': 0.48209,
'Morocco': 0.46473,
'Serbia': 0.41295,
'Japan': 0.34492,
'Canada': 0.36708,
'Poland': 0.3792,
'South Korea': 0.35636,
'Tunisia': 0.30862,
'Iran': 0.34207,
'Wales': 0.32414,
'Cameroon': 0.19799,
'Saudi Arabia': 0.24449,
'Australia': 0.21617,
'Qatar': 0.21656,
'Ghana': 0.18003,
'Costa Rica': 0.08398}