The site says only n=1 and n=2 are proved optimal, so in theory this is an "open problem". But unlike most open math problems posted here, it seems simple enough that someone in the comments could produce a proof. Manifold, I'm counting on you!

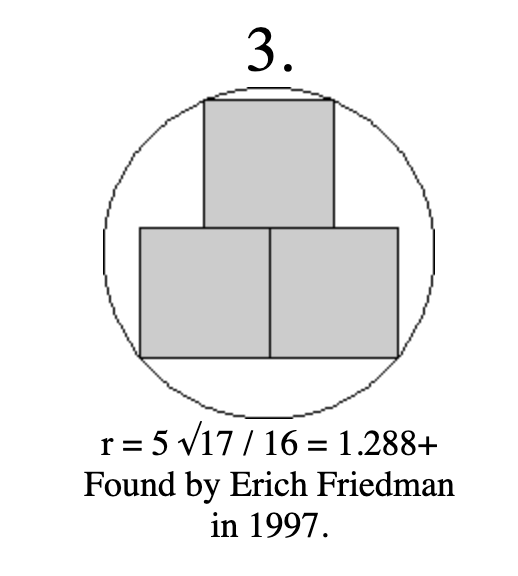
https://erich-friedman.github.io/packing/squincir/

Is the depicted configuration optimal, in the sense that it gives the smallest radius circle in which three unit squares can be packed? 

Market to be extended until a proof is provided.

People are also trading

Related questions