All comments from the last post that I haven't solved are included. However, time spent on those questions during that market and before this one does not count.
🏅 Top traders
| # | Trader | Total profit |
|---|---|---|
| 1 | Ṁ43 | |
| 2 | Ṁ21 | |
| 3 | Ṁ14 | |
| 4 | Ṁ4 | |
| 5 | Ṁ1 |
People are also trading
You are given a set of scales and 12 marbles. The scales are of the old balance variety. That is, a small dish hangs from each end of a rod that is balanced in the middle. The device enables you to conclude either that the contents of the dishes weigh the same or that the dish that falls lower has heavier contents than the other.
The 12 marbles appear to be identical. In fact, 11 of them are identical, and one is of a different weight. Your task is to identify the unusual marble and discard it. You are allowed to use the scales three times if you wish, but no more.
Note that the unusual marble may be heavier or lighter than the others. You are asked to both identify it and determine whether it is heavy or light.
I've also done this before! The scale gives you three distinguishable outcomes. Using it three times means that there are only 27 possible results, so any decision tree can only distinguish 27 initial configurations. There are 24 configurations!
Intuitively, you want each node in the tree to split the configuration-space into thirds, as much as possible. So for our first weighing, we want 8 configurations to result in 'left heavier', 8 to result in 'right heavier', and 8 to result in 'equal weight'. Each child node of that needs <=3 children
i checked the following algorithm in code
So, we weigh marbles 1-4 against marbles 5-8. If 1-4 are heavier, then either the unique marble is 1-4 and heavier or 5-8 and lighter. 5-8 is same WLOG. If equal, the unique marble is in 9-12.
In the first case, weigh A=[1, 5, 9] against B=[2, 6, 7]. Case breakdown: (1H/L: 1 heavier/lighter / A: left heavier, B: right heavier, E=equal)
1H: A 2H: B 3H: E 4H: E 5L: B 6L: A 7L: A 8L: E
Case A: [1H,6L,7L] so weigh 6 and 7, lower wins, if equal 1H wins
Case B: 2H, 5L, compare 1 to 5, if different then 5L otherwise 2H
Case E: 3H, 4H, 8L - compare 3 and 4, higher wins, if equal 8L wins
In the last case, weigh A = [9, 10] against B = [1,12] so we get
9H: A 10H: A 11H: E 12H: B 9L: B 10L: B 11L: E 12L: A
Case A - 9H, 10H, 12L so compare 9 and 10, higher wins, otherwise 12L
Case B - 12H, 9L, 10L - compare 9 and 10, lower wins, otherwise 12H
Case E: 11H, 11L so compare 1 and 11 and it wins
You have 52 playing cards (26 red, 26 black). You draw cards one by one. A red card pays you a dollar. A black one fines you a dollar. You can stop any time you want. Cards are not returned to the deck after being drawn. What is the optimal stopping rule in terms of maximizing expected payoff?
Also, what is the expected payoff following this optimal rule?
I think I've done this one before after seeing it online (maybe it was a similar problem but not the same one), but I don't remember anything about the solution lol
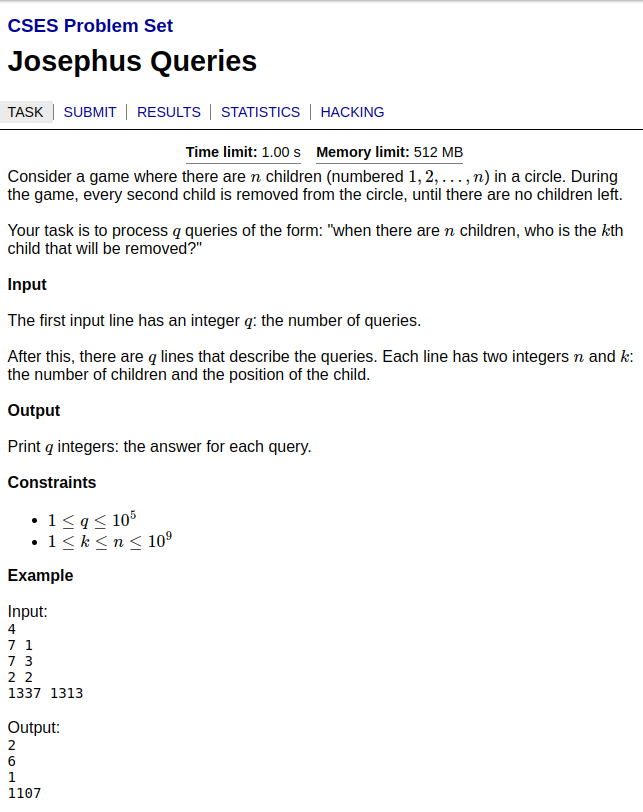
@jacksonpolack https://cses.fi/problemset/task/1653 if you can do this one in less than an hour I'd be quite impressed
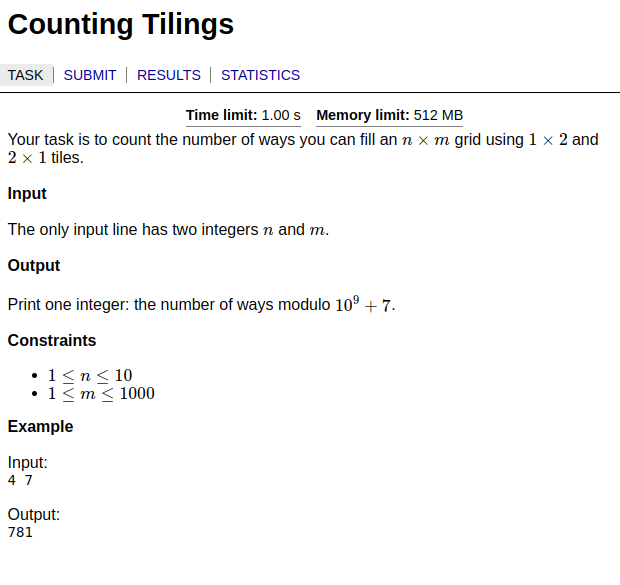
@jacksonpolack https://cses.fi/problemset/task/1625 I'm almost certain you'll take more than an hour for this one if you haven't seen it before
I actually did these a week ago and then forgot to comment so I forget what the literal time complexity was, but iirc the solution I submitted computed a sparse transition matrix and then repeatedly applied to an initial vector, but there was another solution I did after that for fun that was slower in constant-time so wouldn't make it through the time+memory rules but turned it into a dense matrix and took a power of it via the repeated-square-and-accumulate method, meaning I could compute answers for m = 10^10 reasonably quickly
I think I just got binpacking, with 59m on my 'isnt the first one just' commnnt, although it probably still has a few bugs