Geometric mean of shares held per trader above 225 at market close?
21
1kṀ14kresolved Apr 1
Resolved
NO1D
1W
1M
ALL
Geometric mean is the nth root of the product, i.e.
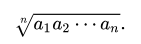
For example, if the market closes like this (cropped for brevity):
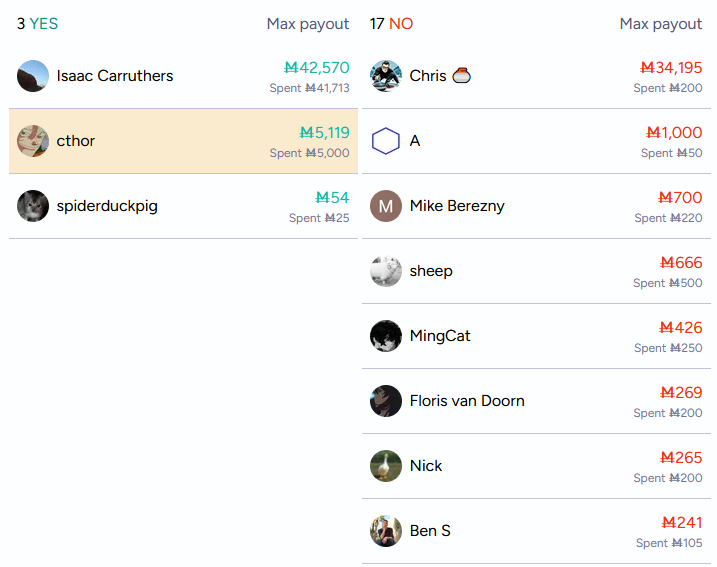
Would resolve YES as 20√(42570 × 5119 × 54 × 34195 × 1000 × 700 × 666 × 426 × 269 × 265 × 241 × 133 × 130 × 125 × 93 × 70 × 64 × 16 × 13 × 13) ≈ 267.
Resolves NO if exactly 225.
Geometric mean is more resistant than arithmetic mean from being influenced by a single large outlier.
I will trade on market but will not withdraw AMM liquidity at any point.
This question is managed and resolved by Manifold.
Get 1,000 to start trading!
1,000 to start trading!
🏅 Top traders
| # | Name | Total profit |
|---|---|---|
| 1 | Ṁ497 | |
| 2 | Ṁ470 | |
| 3 | Ṁ337 | |
| 4 | Ṁ130 | |
| 5 | Ṁ98 |
Related questions
Related questions
Will the median number of shares held in this market exceed 50?
10% chance
Will a NO trader hold more shares than highest YES trader at market close?
49% chance
Will the MEDIAN number of shares held by traders of this market be less than 200?
89% chance
Will the median number of shares held in this market be greater than the modal number of shares?
11% chance