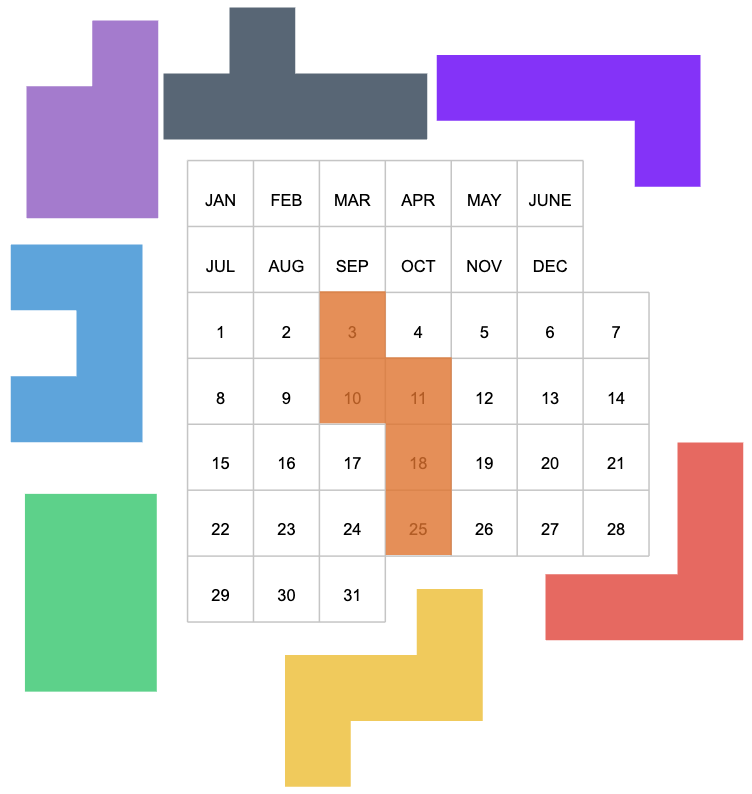
Calendar Puzzle: calpuz.replit.app
For every date either find a solution or show that one doesn't exist.
🏅 Top traders
| # | Trader | Total profit |
|---|---|---|
| 1 | Ṁ93 | |
| 2 | Ṁ40 | |
| 3 | Ṁ30 | |
| 4 | Ṁ8 | |
| 5 | Ṁ4 |
People are also trading
@dreev is there any update in another location about this market? It's currently trading at 74% but no one has commented in quite some time. With only a month to go, time seems to be running out.
Thanks!
Thoughts on representing the state of a partially completed puzzle:
There are 8 pieces, each of which has a position on the board, a rotation, and a chirality. If the piece is not on the board yet, those are null.
There are 12+31 = 43 positions.
Each piece has a focal cell, chosen arbitrarily. Like the orange piece's focal cell is the topmost one in the image below, on the position marked "3". Now we try:
for each position pos on the board:
for each piece pie not yet on the board:
for each rotation rot of pie:
put the focal cell of pie at pos;
count it as a valid successor state if it can be placed there with no overlaps or overhang
So that would be a branching factor of up to 43×8×4×2 = 2752 but most of those are pruned for hanging off the board or overlapping another piece or being a duplicate (e.g., the green piece has just 2 distinct rotations and 1 chirality).