
Ever since Penrose found a two-shape aperiodic tiling of the plane in 1975, mathematicians have wondered if a single shape would suffice. We got our answer on March 20th when Smith, Myers, Kaplan, and Goodman-Strauss published their discovery of The Einstein Hat, the first known aperiodic monotile.
What they actually discovered was an infinite family of aperiodic monotiles. See the neat animation at this timestamped link. There's a Hat, there's a Turtle, and there's an infinite number of other combinatorially equivalent tiles that also tile aperiodically.
This market will resolve YES if a new (combinatorially distinct) family of aperiodic monotiles is discovered by the close date. I will wait for a peer-reviewed result before resolving.
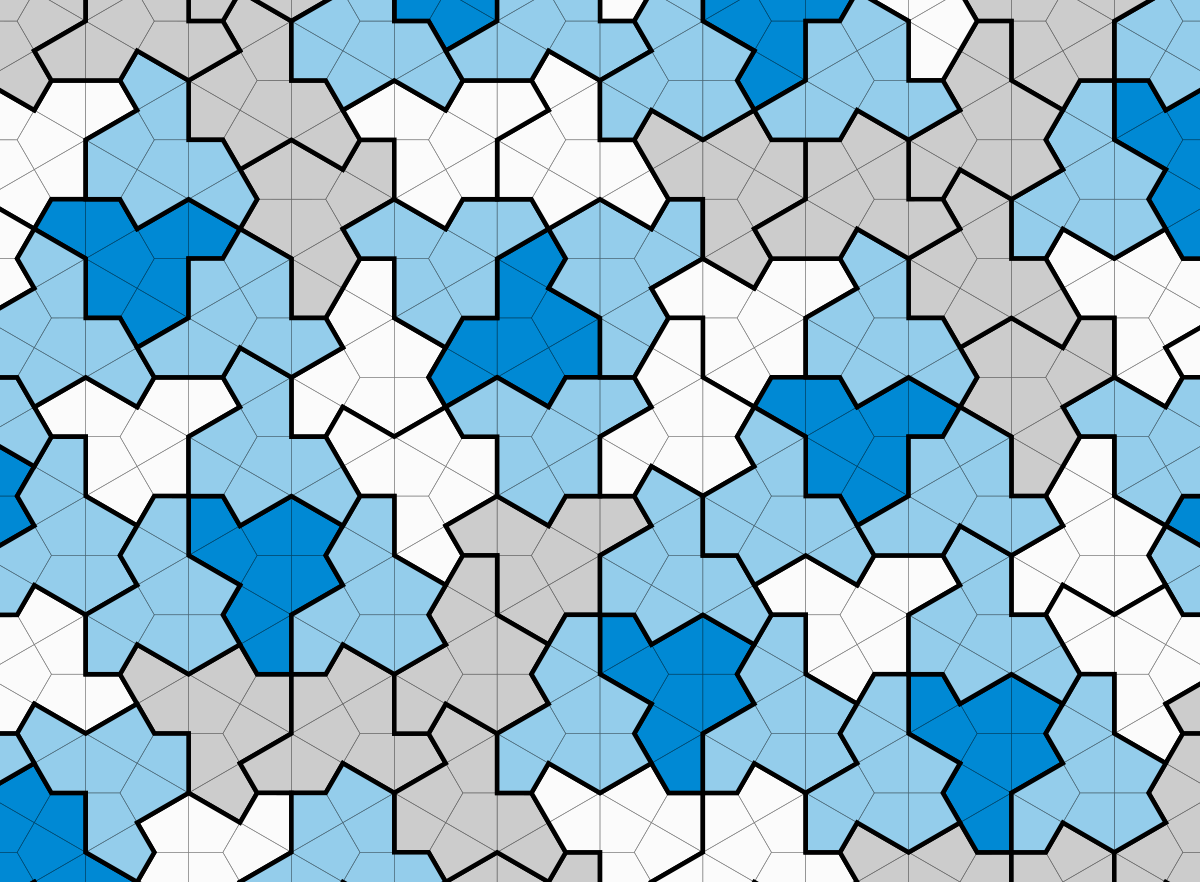
@JimHays I haven’t finished reading the Spectre paper, but doesn’t Spectre belong to the same parameterized family described in the Einstein Hat paper?
The polygon version on the left below is combinatorial equivalent to turtle/hat (they state that in figure 3.1). I don’t think the spectres are because they don’t allow reflections, but I’m not certain, and I’ll leave that for you to determine.
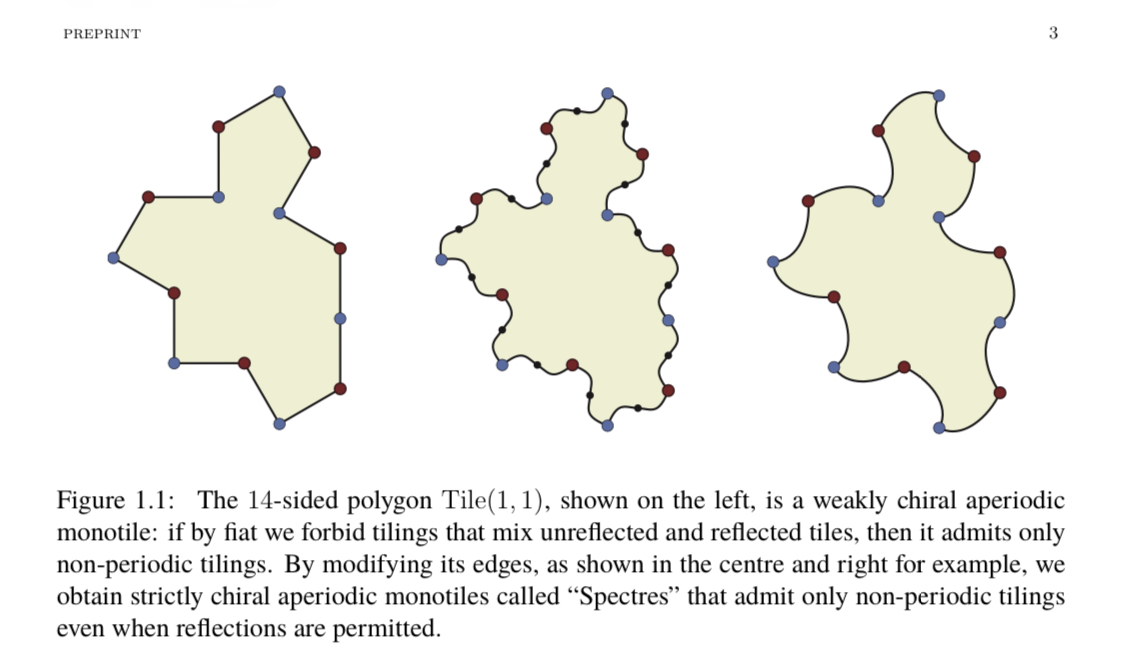
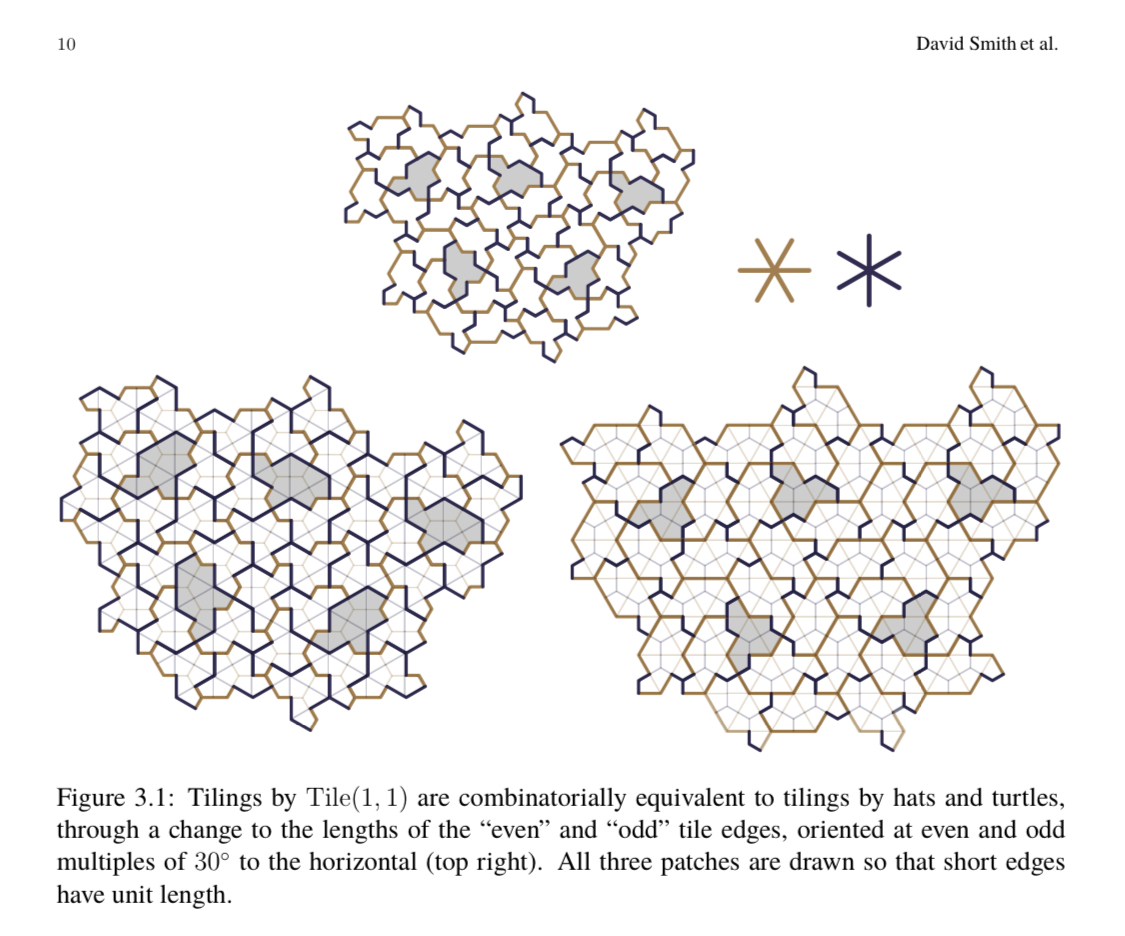
@JimHays I do. The Spectre tiles are from the same parameterized family as the Hat and the Turtle, so I don't consider them a distinct new aperiodic monotile.
@alangrow Can you please clarify what you mean by "combinatorially distinct" then? It can mean different things in different cases, but generally the exact definition is chosen to fit the bill of "is different wrt some combinatorial property we care about". And in the context of tiling "being a chiral aperiodic monotile" sure does look like a combinatorial property we care about.
And Spectre being in the same family isn't technically correct, since as far as I understand, 1) All Tile(x,y) are polygons, and Specter is not; 2) Specter is made from Tile(1,1) which isn't a member of the family since it allows periodic tilings (probably due to that 180 degrees angle).
I mean, I also would like a more distinct tile. And I do expect that a more distinct tile will arrive before 2030. But I think this market must be much more clear about which tiles can resolve it with YES. And it probably should resolve with YES already since I don't see how reasonable definition of "combinatorially distinct" can allow for turtle and specter to be the same thing.
@AlekseyVoropaev You're right that "combinatorially distinct" wasn't well defined or particularly helpful.
I was trying to capture the intuition that, if the Hat can be continuously deformed into some other shape X, and all the shapes along the way admit aperiodic monotiling, then the Hat, X, and everything in between should be considered part of the same family. I did use the language "family of aperiodic monotiles" in the original criteria.
If this is still too handwavey or flat out incorrect in the descriptive sense, maybe you could help me come up with more rigorous criteria.
I don't intend to bet in this market, but my personal opinion is that we're very likely to see a new family of aperiodic monotiles discovered in the coming months or years.
@alangrow > can be continuously deformed into some other shape X, and all the shapes along the way admit aperiodic monotiling;
That is weaker than "combinatorially distinct", e.g. maybe there is a tile 1 that has two aperiodic tilings, but after you deform it into tile 2 it'll have only one aperiodic tiling.
What is more problematic though is that I don't see an easy way of checking whether it is true. E.g. the described in the paper way of going from turtle to specter passes from tile(1,1) which has periodic tiling. But maybe there is some other deformation that passes only through aperiodic monotiles? I would be surprised if authors of those papers know whether such deformation exists.
I suspect* that with some reasonable restrictions on deformation (~ we are changing only finite amount of parameters) it'd need to pass through a tile that (1) has aperiodic tiling with some tiles flipped and (2) has aperiodic tiling with no tiles flipped, but (3) no periodic tilings. And I think if such tile was known, we would've heard about it (turtle has 1,3; specter has 2,3; tile(1,1) has 1,2).
I want to read those papers soon, so maybe in a week I'll have more evidence about whether something is known about the existence of such deformation.
By the way, have you watched videos where authors describe ideas they used when proving that turtle and specter are aperiodic monotiles? It seems to me that you assume that the latter was proven by smth like "specter is a member of some family => it's aperiodic monotile", while my impression is that it were more like "we'll prove it from the scratch using the same methods we used for turtle".
https://www.youtube.com/watch?v=FkZPMf73qYc
https://www.youtube.com/watch?v=OImGgciDZ_A (at ~12:28)
* Rough, likely incorrect idea of how it can be proven:
Turtle has only tilings with flips. Specter has only tilings with no flips. The property "has tilings with flips" looks like something that will induce a closed set on the path from turtle to specter. Same for the property "has tilings with no flips". Since every tile on the path must have at least one of the two, and the endpoints have different properties, those closed sets must intersect, and all tiles in that intersection will have both properties.
