Start with a grid of nodes that's X nodes across and Y nodes high. You're going to draw a path starting at any node on the left edge and ending at any node on the right edge. The path can only move from a node to a directly adjacent node in the vertical or horizontal direction, and it cannot touch any node twice. (It may leave a node untouched.) How many total paths are there?
When X is 1, the total number of paths is Y^2.
When Y is 1, the total number of paths is 1.
When Y is 2, the number of total paths is 2^(X+1).
For any Y > 2, Y^(X+1) is a lower bound, but the actual number of paths is much higher.
I will leave proving all of the above statements as an exercise to the reader. Past these numbers, it becomes... challenging. I want a closed-form expression for Y=3, which is restricted enough that I feel like it's still possible.
The general case where X and Y can vary arbitrarily and the path can start and end at any node has been widely studied and no solution is known.
🏅 Top traders
| # | Name | Total profit |
|---|---|---|
| 1 | Ṁ230 | |
| 2 | Ṁ114 | |
| 3 | Ṁ23 | |
| 4 | Ṁ21 | |
| 5 | Ṁ18 |
@Tasty_Y Can you elaborate on that? What part of it doesn't work? i.e. if I used your formula, would the answer be wrong?
@IsaacKing Ok, see:
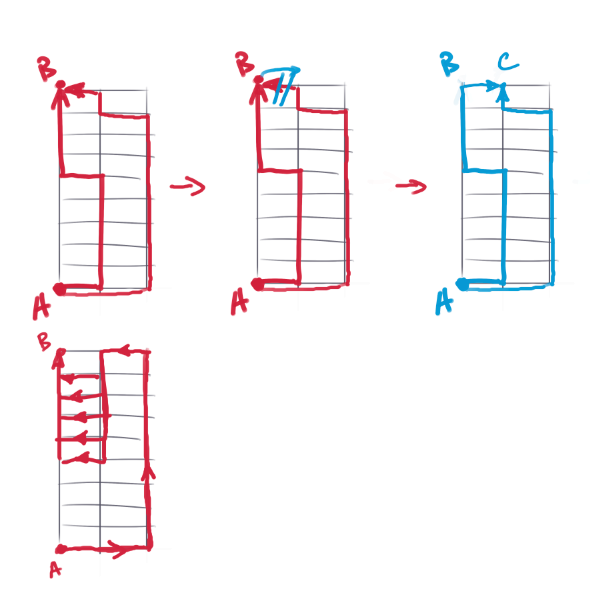
we know how to count all the red-type paths (going from A to B). We want to count all the blue paths (going from A to C). I thought the number would be the same, because you can turn the red paths into blue ones by slightly adjusting the last step they make, adding or deleting one. But this was not right, because there's a bunch of red paths that can't be turned into blue paths this simply. Maybe the argument can be somehow fixed and the idea can be made to work, but I don't see exactly how now, certainly didn't see when I first wrote the comment, so if the formula works at all, it's by sheer luck and shouldn't count.
I still think that finding the right formula using the methods in the paper I showed should be doable, but I'm not up for it.
@oh Oh yeah. I need to go through the formula provided and figure out if it's what I wanted; haven't done that yet.
Here's the information you need to put together the formula: there's a known solution for a very similar problem, where you travel not from edge to edge, but from one corner to another corner: https://oeis.org/A006189
There's a paper that explains how the formula was derived: https://oeis.org/A006189/a006189.pdf
It seems like if you tweak their method slightly you'll have all the components to get the formula for the number of side-to-side walks.
@Tasty_Y Oh, neat! This provides a new lower bound that's better than my old one, though still much lower than the true value.
The fact that they're traveling from top to bottom rather than edge to edge is irrelevant; you just rotate the matrix by 90 degrees. A bigger issue is that they're restricting their path to start and end on the edge of the rectangle, which doesn't have an obvious isomorphism to starting/ending in the middle. I haven't read the full paper though, so their method might still be able to handle that. (But I imagine there was some reason they restricted their paper to cover only the edge version?)
@IsaacKing If I'm not making a silly mistake, I think it's like this: you have a formula f(x) for how many paths start in the, let's call it lower left corner and end in upper left corner. You want to know how many paths start somewhere on the bottom edge and end somewhere on the top edge.
So all these paths that you want to count can be divided into groups.
start in the lower left, end in the upper left - that's f(x), we know that.
start in the lower left, end in the center - I think it's the same number f(x) because you can get all these paths from the paths in group (1) by shortening or extending them slightly, and it's a 1-to-1 correspondence.
start in the lower left end in the upper left - also f(x).
so the number of the paths that start in the lower left and get to the top is 3f(x).
By symmetry, the number of the paths that start in the lower right and get to the top is also 3f(x), so 6f(x) so far.
the paths that start in the middle:
4.1 there are 3 paths that start in the middle and stay in the middle and never hit the sides until the very end.
4.2 there are paths that start in the middle, stay in the middle for n steps, then hit the side. Once they hit the side, they must make one step up. from there they can reach the top however they want, but this is just the initial problem starting at the side covered by points 1-3, so they can ascend in 6f(x-n) ways. And you sum this by n from something to something else.
So I guess the end result is something like 6f(x)+3+sum (i=1...x-1) 6f(x-n) and that's the answer.
Warning: the above reasoning probably contains some errors, I didn't think it through 100%, but the right answer is something along those lines.
@Tasty_Y That all seems correct to me!
What exactly is f? I've having trouble finding it. (Don't have a lot of time to read though everything right now.)
@IsaacKing I'm pretty sure I'm off by one in a bunch of places in there. f(x) is:
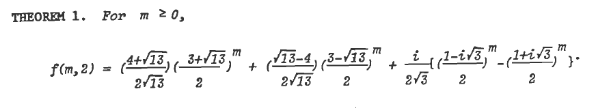
in the paper and in the post it's
a(n) = (1/2)*( ChebyshevU(n, 1/2) - ChebyshevU(n-1, 1/2) + i^n*( ChebyshevU(n, -3*i/2) + i*ChebyshevU(n-1, -3*i/2) ) ) which I imagine is the same.
@IsaacKing They obtain the formula by first proving a recursive formula f(n) = 4*f(n-1) - 3*f(n-2) + 2*f(n-3) + f(n-4). Then they apply a common technique for getting an explicit formula from a recursive one https://www.cl.cam.ac.uk/teaching/2003/Probability/prob07.pdf, and to do that you use the roots of the algebraic equation you produce along the way. 13 comes from one of those roots. Same way that 5 appears in the explicit formula for the Fibonacci numbers.
Do you have a table of pre-calculated values? Would help with verification.