An experiment with benford's law.
https://en.m.wikipedia.org/wiki/Benford%27s_law
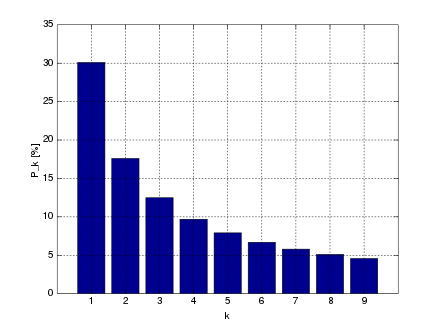
Benford's law assumes the log of the final number is distributed uniformly.
If we put an upper or lower bound on what the answer can be, we can calculate a distribution based on that (for example if there is already 500M spent on the market and we don't think it will ever go higher than 10,000M, then first digits 1-4 are less likely because we're already up to 500).
I've made a spreadsheet to calculate this here:
I've shared as view only, but you should be able to make a copy of the spreadsheet and put in your own numbers.
1,000🏅 Top traders
| # | Name | Total profit |
|---|---|---|
| 1 | Ṁ251 | |
| 2 | Ṁ50 | |
| 3 | Ṁ3 | |
| 4 | Ṁ1 |
Benford's law assumes the log of the final number is distributed uniformly.
If we put an upper or lower bound on what the answer can be, we can calculate a distribution based on that (for example if there is already 500M spent on the market and we don't think it will ever go higher than 10,000M, then first digits 1-4 are less likely because we're already up to 500).
I've made a spreadsheet to calculate this here:
@Daniel_MC I've shared as view only, but you should be able to make a copy of the spreadsheet and put in your own numbers